Del in cylindrical and spherical coordinates Last updated July 27, 2024 Notes This article uses the standard notation ISO 80000-2 , which supersedes ISO 31-11 , for spherical coordinates (other sources may reverse the definitions of θ and φ ): The polar angle is denoted by θ ∈ [ 0 , π ] {\displaystyle \theta \in [0,\pi ]} z -axis and the radial vector connecting the origin to the point in question. The azimuthal angle is denoted by φ ∈ [ 0 , 2 π ] {\displaystyle \varphi \in [0,2\pi ]} x -axis and the projection of the radial vector onto the xy -plane. The function atan2 (y , x ) can be used instead of the mathematical function arctan (y /x ) owing to its domain and image . The classical arctan function has an image of (−π/2, +π/2) , whereas atan2 is defined to have an image of (−π, π] . Unit vector conversions Conversion between unit vectors in Cartesian, cylindrical, and spherical coordinate systems in terms of destination coordinates [1] Cartesian Cylindrical Spherical Cartesian x ^ = x ^ y ^ = y ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\hat {\mathbf {x} }}\\{\hat {\mathbf {y} }}&={\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} x ^ = cos φ ρ ^ − sin φ φ ^ y ^ = sin φ ρ ^ + cos φ φ ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&=\cos \varphi {\hat {\boldsymbol {\rho }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \varphi {\hat {\boldsymbol {\rho }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} x ^ = sin θ cos φ r ^ + cos θ cos φ θ ^ − sin φ φ ^ y ^ = sin θ sin φ r ^ + cos θ sin φ θ ^ + cos φ φ ^ z ^ = cos θ r ^ − sin θ θ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&=\sin \theta \cos \varphi {\hat {\mathbf {r} }}+\cos \theta \cos \varphi {\hat {\boldsymbol {\theta }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \theta \sin \varphi {\hat {\mathbf {r} }}+\cos \theta \sin \varphi {\hat {\boldsymbol {\theta }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}} Cylindrical ρ ^ = x x ^ + y y ^ x 2 + y 2 φ ^ = − y x ^ + x y ^ x 2 + y 2 z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} ρ ^ = ρ ^ φ ^ = φ ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\hat {\boldsymbol {\rho }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} ρ ^ = sin θ r ^ + cos θ θ ^ φ ^ = φ ^ z ^ = cos θ r ^ − sin θ θ ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\sin \theta {\hat {\mathbf {r} }}+\cos \theta {\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}} Spherical r ^ = x x ^ + y y ^ + z z ^ x 2 + y 2 + z 2 θ ^ = ( x x ^ + y y ^ ) z − ( x 2 + y 2 ) z ^ x 2 + y 2 + z 2 x 2 + y 2 φ ^ = − y x ^ + x y ^ x 2 + y 2 {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}+z{\hat {\mathbf {z} }}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {\left(x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}\right)z-\left(x^{2}+y^{2}\right){\hat {\mathbf {z} }}}{{\sqrt {x^{2}+y^{2}+z^{2}}}{\sqrt {x^{2}+y^{2}}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\end{aligned}}} r ^ = ρ ρ ^ + z z ^ ρ 2 + z 2 θ ^ = z ρ ^ − ρ z ^ ρ 2 + z 2 φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\frac {\rho {\hat {\boldsymbol {\rho }}}+z{\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {z{\hat {\boldsymbol {\rho }}}-\rho {\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}} r ^ = r ^ θ ^ = θ ^ φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\hat {\mathbf {r} }}\\{\hat {\boldsymbol {\theta }}}&={\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\\end{aligned}}}
Conversion between unit vectors in Cartesian, cylindrical, and spherical coordinate systems in terms of source coordinates Cartesian Cylindrical Spherical Cartesian x ^ = x ^ y ^ = y ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\hat {\mathbf {x} }}\\{\hat {\mathbf {y} }}&={\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} x ^ = x ρ ^ − y φ ^ x 2 + y 2 y ^ = y ρ ^ + x φ ^ x 2 + y 2 z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x{\hat {\boldsymbol {\rho }}}-y{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {y} }}&={\frac {y{\hat {\boldsymbol {\rho }}}+x{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} x ^ = x ( x 2 + y 2 r ^ + z θ ^ ) − y x 2 + y 2 + z 2 φ ^ x 2 + y 2 x 2 + y 2 + z 2 y ^ = y ( x 2 + y 2 r ^ + z θ ^ ) + x x 2 + y 2 + z 2 φ ^ x 2 + y 2 x 2 + y 2 + z 2 z ^ = z r ^ − x 2 + y 2 θ ^ x 2 + y 2 + z 2 {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)-y{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {y} }}&={\frac {y\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)+x{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-{\sqrt {x^{2}+y^{2}}}{\hat {\boldsymbol {\theta }}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\end{aligned}}} Cylindrical ρ ^ = cos φ x ^ + sin φ y ^ φ ^ = − sin φ x ^ + cos φ y ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} ρ ^ = ρ ^ φ ^ = φ ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\hat {\boldsymbol {\rho }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} ρ ^ = ρ r ^ + z θ ^ ρ 2 + z 2 φ ^ = φ ^ z ^ = z r ^ − ρ θ ^ ρ 2 + z 2 {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {\rho {\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-\rho {\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\end{aligned}}} Spherical r ^ = sin θ ( cos φ x ^ + sin φ y ^ ) + cos θ z ^ θ ^ = cos θ ( cos φ x ^ + sin φ y ^ ) − sin θ z ^ φ ^ = − sin φ x ^ + cos φ y ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\end{aligned}}} r ^ = sin θ ρ ^ + cos θ z ^ θ ^ = cos θ ρ ^ − sin θ z ^ φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta {\hat {\boldsymbol {\rho }}}+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta {\hat {\boldsymbol {\rho }}}-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}} r ^ = r ^ θ ^ = θ ^ φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\hat {\mathbf {r} }}\\{\hat {\boldsymbol {\theta }}}&={\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\\end{aligned}}}
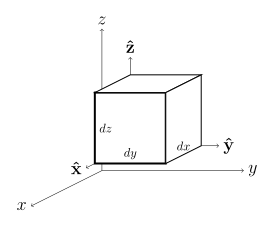
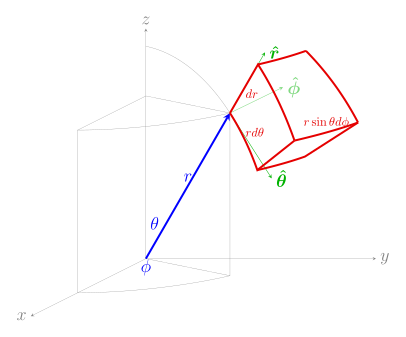
Table with the del operator in cartesian, cylindrical and spherical coordinates Operation Cartesian coordinates (x , y , z ) Cylindrical coordinates (ρ , φ , z ) Spherical coordinates (r , θ , φ ) ,θ φ α Vector field A A x x ^ + A y y ^ + A z z ^ {\displaystyle A_{x}{\hat {\mathbf {x} }}+A_{y}{\hat {\mathbf {y} }}+A_{z}{\hat {\mathbf {z} }}} A ρ ρ ^ + A φ φ ^ + A z z ^ {\displaystyle A_{\rho }{\hat {\boldsymbol {\rho }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}+A_{z}{\hat {\mathbf {z} }}} A r r ^ + A θ θ ^ + A φ φ ^ {\displaystyle A_{r}{\hat {\mathbf {r} }}+A_{\theta }{\hat {\boldsymbol {\theta }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}} Gradient ∇f [1] ∂ f ∂ x x ^ + ∂ f ∂ y y ^ + ∂ f ∂ z z ^ {\displaystyle {\partial f \over \partial x}{\hat {\mathbf {x} }}+{\partial f \over \partial y}{\hat {\mathbf {y} }}+{\partial f \over \partial z}{\hat {\mathbf {z} }}} ∂ f ∂ ρ ρ ^ + 1 ρ ∂ f ∂ φ φ ^ + ∂ f ∂ z z ^ {\displaystyle {\partial f \over \partial \rho }{\hat {\boldsymbol {\rho }}}+{1 \over \rho }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}+{\partial f \over \partial z}{\hat {\mathbf {z} }}} ∂ f ∂ r r ^ + 1 r ∂ f ∂ θ θ ^ + 1 r sin θ ∂ f ∂ φ φ ^ {\displaystyle {\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}} Divergence ∇ ⋅ A [1] ∂ A x ∂ x + ∂ A y ∂ y + ∂ A z ∂ z {\displaystyle {\partial A_{x} \over \partial x}+{\partial A_{y} \over \partial y}+{\partial A_{z} \over \partial z}} 1 ρ ∂ ( ρ A ρ ) ∂ ρ + 1 ρ ∂ A φ ∂ φ + ∂ A z ∂ z {\displaystyle {1 \over \rho }{\partial \left(\rho A_{\rho }\right) \over \partial \rho }+{1 \over \rho }{\partial A_{\varphi } \over \partial \varphi }+{\partial A_{z} \over \partial z}} 1 r 2 ∂ ( r 2 A r ) ∂ r + 1 r sin θ ∂ ∂ θ ( A θ sin θ ) + 1 r sin θ ∂ A φ ∂ φ {\displaystyle {1 \over r^{2}}{\partial \left(r^{2}A_{r}\right) \over \partial r}+{1 \over r\sin \theta }{\partial \over \partial \theta }\left(A_{\theta }\sin \theta \right)+{1 \over r\sin \theta }{\partial A_{\varphi } \over \partial \varphi }} Curl ∇ × A [1] ( ∂ A z ∂ y − ∂ A y ∂ z ) x ^ + ( ∂ A x ∂ z − ∂ A z ∂ x ) y ^ + ( ∂ A y ∂ x − ∂ A x ∂ y ) z ^ {\displaystyle {\begin{aligned}\left({\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\right)&{\hat {\mathbf {x} }}\\+\left({\frac {\partial A_{x}}{\partial z}}-{\frac {\partial A_{z}}{\partial x}}\right)&{\hat {\mathbf {y} }}\\+\left({\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}\right)&{\hat {\mathbf {z} }}\end{aligned}}} ( 1 ρ ∂ A z ∂ φ − ∂ A φ ∂ z ) ρ ^ + ( ∂ A ρ ∂ z − ∂ A z ∂ ρ ) φ ^ + 1 ρ ( ∂ ( ρ A φ ) ∂ ρ − ∂ A ρ ∂ φ ) z ^ {\displaystyle {\begin{aligned}\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right)&{\hat {\boldsymbol {\rho }}}\\+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\+{\frac {1}{\rho }}\left({\frac {\partial \left(\rho A_{\varphi }\right)}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \varphi }}\right)&{\hat {\mathbf {z} }}\end{aligned}}} 1 r sin θ ( ∂ ∂ θ ( A φ sin θ ) − ∂ A θ ∂ φ ) r ^ + 1 r ( 1 sin θ ∂ A r ∂ φ − ∂ ∂ r ( r A φ ) ) θ ^ + 1 r ( ∂ ∂ r ( r A θ ) − ∂ A r ∂ θ ) φ ^ {\displaystyle {\begin{aligned}{\frac {1}{r\sin \theta }}\left({\frac {\partial }{\partial \theta }}\left(A_{\varphi }\sin \theta \right)-{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\{}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {\partial }{\partial r}}\left(rA_{\varphi }\right)\right)&{\hat {\boldsymbol {\theta }}}\\{}+{\frac {1}{r}}\left({\frac {\partial }{\partial r}}\left(rA_{\theta }\right)-{\frac {\partial A_{r}}{\partial \theta }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}} Laplace operator ∇2 f ≡ ∆f [1] ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 + ∂ 2 f ∂ z 2 {\displaystyle {\partial ^{2}f \over \partial x^{2}}+{\partial ^{2}f \over \partial y^{2}}+{\partial ^{2}f \over \partial z^{2}}} 1 ρ ∂ ∂ ρ ( ρ ∂ f ∂ ρ ) + 1 ρ 2 ∂ 2 f ∂ φ 2 + ∂ 2 f ∂ z 2 {\displaystyle {1 \over \rho }{\partial \over \partial \rho }\left(\rho {\partial f \over \partial \rho }\right)+{1 \over \rho ^{2}}{\partial ^{2}f \over \partial \varphi ^{2}}+{\partial ^{2}f \over \partial z^{2}}} 1 r 2 ∂ ∂ r ( r 2 ∂ f ∂ r ) + 1 r 2 sin θ ∂ ∂ θ ( sin θ ∂ f ∂ θ ) + 1 r 2 sin 2 θ ∂ 2 f ∂ φ 2 {\displaystyle {1 \over r^{2}}{\partial \over \partial r}\!\left(r^{2}{\partial f \over \partial r}\right)\!+\!{1 \over r^{2}\!\sin \theta }{\partial \over \partial \theta }\!\left(\sin \theta {\partial f \over \partial \theta }\right)\!+\!{1 \over r^{2}\!\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}} Vector gradient ∇A β ∂ A x ∂ x x ^ ⊗ x ^ + ∂ A x ∂ y x ^ ⊗ y ^ + ∂ A x ∂ z x ^ ⊗ z ^ + ∂ A y ∂ x y ^ ⊗ x ^ + ∂ A y ∂ y y ^ ⊗ y ^ + ∂ A y ∂ z y ^ ⊗ z ^ + ∂ A z ∂ x z ^ ⊗ x ^ + ∂ A z ∂ y z ^ ⊗ y ^ + ∂ A z ∂ z z ^ ⊗ z ^ {\displaystyle {\begin{aligned}{}&{\frac {\partial A_{x}}{\partial x}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{x}}{\partial y}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{x}}{\partial z}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{y}}{\partial x}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{y}}{\partial y}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{y}}{\partial z}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{z}}{\partial x}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{z}}{\partial y}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{z}}{\partial z}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {z} }}\end{aligned}}} ∂ A ρ ∂ ρ ρ ^ ⊗ ρ ^ + ( 1 ρ ∂ A ρ ∂ φ − A φ ρ ) ρ ^ ⊗ φ ^ + ∂ A ρ ∂ z ρ ^ ⊗ z ^ + ∂ A φ ∂ ρ φ ^ ⊗ ρ ^ + ( 1 ρ ∂ A φ ∂ φ + A ρ ρ ) φ ^ ⊗ φ ^ + ∂ A φ ∂ z φ ^ ⊗ z ^ + ∂ A z ∂ ρ z ^ ⊗ ρ ^ + 1 ρ ∂ A z ∂ φ z ^ ⊗ φ ^ + ∂ A z ∂ z z ^ ⊗ z ^ {\displaystyle {\begin{aligned}{}&{\frac {\partial A_{\rho }}{\partial \rho }}{\hat {\boldsymbol {\rho }}}\otimes {\hat {\boldsymbol {\rho }}}+\left({\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \varphi }}-{\frac {A_{\varphi }}{\rho }}\right){\hat {\boldsymbol {\rho }}}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{\rho }}{\partial z}}{\hat {\boldsymbol {\rho }}}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{\varphi }}{\partial \rho }}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\rho }}}+\left({\frac {1}{\rho }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {A_{\rho }}{\rho }}\right){\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{\varphi }}{\partial z}}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{z}}{\partial \rho }}{\hat {\mathbf {z} }}\otimes {\hat {\boldsymbol {\rho }}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}{\hat {\mathbf {z} }}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{z}}{\partial z}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {z} }}\end{aligned}}} ∂ A r ∂ r r ^ ⊗ r ^ + ( 1 r ∂ A r ∂ θ − A θ r ) r ^ ⊗ θ ^ + ( 1 r sin θ ∂ A r ∂ φ − A φ r ) r ^ ⊗ φ ^ + ∂ A θ ∂ r θ ^ ⊗ r ^ + ( 1 r ∂ A θ ∂ θ + A r r ) θ ^ ⊗ θ ^ + ( 1 r sin θ ∂ A θ ∂ φ − cot θ A φ r ) θ ^ ⊗ φ ^ + ∂ A φ ∂ r φ ^ ⊗ r ^ + 1 r ∂ A φ ∂ θ φ ^ ⊗ θ ^ + ( 1 r sin θ ∂ A φ ∂ φ + cot θ A θ r + A r r ) φ ^ ⊗ φ ^ {\displaystyle {\begin{aligned}{}&{\frac {\partial A_{r}}{\partial r}}{\hat {\mathbf {r} }}\otimes {\hat {\mathbf {r} }}+\left({\frac {1}{r}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {A_{\theta }}{r}}\right){\hat {\mathbf {r} }}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {A_{\varphi }}{r}}\right){\hat {\mathbf {r} }}\otimes {\hat {\boldsymbol {\varphi }}}\\{}+&{\frac {\partial A_{\theta }}{\partial r}}{\hat {\boldsymbol {\theta }}}\otimes {\hat {\mathbf {r} }}+\left({\frac {1}{r}}{\frac {\partial A_{\theta }}{\partial \theta }}+{\frac {A_{r}}{r}}\right){\hat {\boldsymbol {\theta }}}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{\theta }}{\partial \varphi }}-\cot \theta {\frac {A_{\varphi }}{r}}\right){\hat {\boldsymbol {\theta }}}\otimes {\hat {\boldsymbol {\varphi }}}\\{}+&{\frac {\partial A_{\varphi }}{\partial r}}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\mathbf {r} }}+{\frac {1}{r}}{\frac {\partial A_{\varphi }}{\partial \theta }}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+\cot \theta {\frac {A_{\theta }}{r}}+{\frac {A_{r}}{r}}\right){\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\varphi }}}\end{aligned}}} Vector Laplacian ∇2 A ≡ ∆A [2] ∇ 2 A x x ^ + ∇ 2 A y y ^ + ∇ 2 A z z ^ {\displaystyle \nabla ^{2}A_{x}{\hat {\mathbf {x} }}+\nabla ^{2}A_{y}{\hat {\mathbf {y} }}+\nabla ^{2}A_{z}{\hat {\mathbf {z} }}} ( ∇ 2 A ρ − A ρ ρ 2 − 2 ρ 2 ∂ A φ ∂ φ ) ρ ^ + ( ∇ 2 A φ − A φ ρ 2 + 2 ρ 2 ∂ A ρ ∂ φ ) φ ^ + ∇ 2 A z z ^ {\displaystyle {\begin{aligned}{\mathopen {}}\left(\nabla ^{2}A_{\rho }-{\frac {A_{\rho }}{\rho ^{2}}}-{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\rho }}}\\+{\mathopen {}}\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{\rho ^{2}}}+{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\varphi }}}\\{}+\nabla ^{2}A_{z}&{\hat {\mathbf {z} }}\end{aligned}}}
( ∇ 2 A r − 2 A r r 2 − 2 r 2 sin θ ∂ ( A θ sin θ ) ∂ θ − 2 r 2 sin θ ∂ A φ ∂ φ ) r ^ + ( ∇ 2 A θ − A θ r 2 sin 2 θ + 2 r 2 ∂ A r ∂ θ − 2 cos θ r 2 sin 2 θ ∂ A φ ∂ φ ) θ ^ + ( ∇ 2 A φ − A φ r 2 sin 2 θ + 2 r 2 sin θ ∂ A r ∂ φ + 2 cos θ r 2 sin 2 θ ∂ A θ ∂ φ ) φ ^ {\displaystyle {\begin{aligned}\left(\nabla ^{2}A_{r}-{\frac {2A_{r}}{r^{2}}}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial \left(A_{\theta }\sin \theta \right)}{\partial \theta }}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\+\left(\nabla ^{2}A_{\theta }-{\frac {A_{\theta }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\theta }}}\\+\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}+{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}
Directional derivative (A ⋅ ∇)B [3] A ⋅ ∇ B x x ^ + A ⋅ ∇ B y y ^ + A ⋅ ∇ B z z ^ {\displaystyle \mathbf {A} \cdot \nabla B_{x}{\hat {\mathbf {x} }}+\mathbf {A} \cdot \nabla B_{y}{\hat {\mathbf {y} }}+\mathbf {A} \cdot \nabla B_{z}{\hat {\mathbf {z} }}} ( A ρ ∂ B ρ ∂ ρ + A φ ρ ∂ B ρ ∂ φ + A z ∂ B ρ ∂ z − A φ B φ ρ ) ρ ^ + ( A ρ ∂ B φ ∂ ρ + A φ ρ ∂ B φ ∂ φ + A z ∂ B φ ∂ z + A φ B ρ ρ ) φ ^ + ( A ρ ∂ B z ∂ ρ + A φ ρ ∂ B z ∂ φ + A z ∂ B z ∂ z ) z ^ {\displaystyle {\begin{aligned}\left(A_{\rho }{\frac {\partial B_{\rho }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\rho }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\rho }}{\partial z}}-{\frac {A_{\varphi }B_{\varphi }}{\rho }}\right)&{\hat {\boldsymbol {\rho }}}\\+\left(A_{\rho }{\frac {\partial B_{\varphi }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\varphi }}{\partial z}}+{\frac {A_{\varphi }B_{\rho }}{\rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\+\left(A_{\rho }{\frac {\partial B_{z}}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{z}}{\partial \varphi }}+A_{z}{\frac {\partial B_{z}}{\partial z}}\right)&{\hat {\mathbf {z} }}\end{aligned}}} ( A r ∂ B r ∂ r + A θ r ∂ B r ∂ θ + A φ r sin θ ∂ B r ∂ φ − A θ B θ + A φ B φ r ) r ^ + ( A r ∂ B θ ∂ r + A θ r ∂ B θ ∂ θ + A φ r sin θ ∂ B θ ∂ φ + A θ B r r − A φ B φ cot θ r ) θ ^ + ( A r ∂ B φ ∂ r + A θ r ∂ B φ ∂ θ + A φ r sin θ ∂ B φ ∂ φ + A φ B r r + A φ B θ cot θ r ) φ ^ {\displaystyle {\begin{aligned}\left(A_{r}{\frac {\partial B_{r}}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{r}}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{r}}{\partial \varphi }}-{\frac {A_{\theta }B_{\theta }+A_{\varphi }B_{\varphi }}{r}}\right)&{\hat {\mathbf {r} }}\\+\left(A_{r}{\frac {\partial B_{\theta }}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{\theta }}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{\theta }}{\partial \varphi }}+{\frac {A_{\theta }B_{r}}{r}}-{\frac {A_{\varphi }B_{\varphi }\cot \theta }{r}}\right)&{\hat {\boldsymbol {\theta }}}\\+\left(A_{r}{\frac {\partial B_{\varphi }}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{\varphi }}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+{\frac {A_{\varphi }B_{r}}{r}}+{\frac {A_{\varphi }B_{\theta }\cot \theta }{r}}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}
Tensor divergence ∇ ⋅ T γ ( ∂ T x x ∂ x + ∂ T y x ∂ y + ∂ T z x ∂ z ) x ^ + ( ∂ T x y ∂ x + ∂ T y y ∂ y + ∂ T z y ∂ z ) y ^ + ( ∂ T x z ∂ x + ∂ T y z ∂ y + ∂ T z z ∂ z ) z ^ {\displaystyle {\begin{aligned}\left({\frac {\partial T_{xx}}{\partial x}}+{\frac {\partial T_{yx}}{\partial y}}+{\frac {\partial T_{zx}}{\partial z}}\right)&{\hat {\mathbf {x} }}\\+\left({\frac {\partial T_{xy}}{\partial x}}+{\frac {\partial T_{yy}}{\partial y}}+{\frac {\partial T_{zy}}{\partial z}}\right)&{\hat {\mathbf {y} }}\\+\left({\frac {\partial T_{xz}}{\partial x}}+{\frac {\partial T_{yz}}{\partial y}}+{\frac {\partial T_{zz}}{\partial z}}\right)&{\hat {\mathbf {z} }}\end{aligned}}}
[ ∂ T ρ ρ ∂ ρ + 1 ρ ∂ T φ ρ ∂ φ + ∂ T z ρ ∂ z + 1 ρ ( T ρ ρ − T φ φ ) ] ρ ^ + [ ∂ T ρ φ ∂ ρ + 1 ρ ∂ T φ φ ∂ φ + ∂ T z φ ∂ z + 1 ρ ( T ρ φ + T φ ρ ) ] φ ^ + [ ∂ T ρ z ∂ ρ + 1 ρ ∂ T φ z ∂ φ + ∂ T z z ∂ z + T ρ z ρ ] z ^ {\displaystyle {\begin{aligned}\left[{\frac {\partial T_{\rho \rho }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \rho }}{\partial \varphi }}+{\frac {\partial T_{z\rho }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \rho }-T_{\varphi \varphi })\right]&{\hat {\boldsymbol {\rho }}}\\+\left[{\frac {\partial T_{\rho \varphi }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {\partial T_{z\varphi }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \varphi }+T_{\varphi \rho })\right]&{\hat {\boldsymbol {\varphi }}}\\+\left[{\frac {\partial T_{\rho z}}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi z}}{\partial \varphi }}+{\frac {\partial T_{zz}}{\partial z}}+{\frac {T_{\rho z}}{\rho }}\right]&{\hat {\mathbf {z} }}\end{aligned}}}
[ ∂ T r r ∂ r + 2 T r r r + 1 r ∂ T θ r ∂ θ + cot θ r T θ r + 1 r sin θ ∂ T φ r ∂ φ − 1 r ( T θ θ + T φ φ ) ] r ^ + [ ∂ T r θ ∂ r + 2 T r θ r + 1 r ∂ T θ θ ∂ θ + cot θ r T θ θ + 1 r sin θ ∂ T φ θ ∂ φ + T θ r r − cot θ r T φ φ ] θ ^ + [ ∂ T r φ ∂ r + 2 T r φ r + 1 r ∂ T θ φ ∂ θ + 1 r sin θ ∂ T φ φ ∂ φ + T φ r r + cot θ r ( T θ φ + T φ θ ) ] φ ^ {\displaystyle {\begin{aligned}\left[{\frac {\partial T_{rr}}{\partial r}}+2{\frac {T_{rr}}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta r}}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta r}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi r}}{\partial \varphi }}-{\frac {1}{r}}(T_{\theta \theta }+T_{\varphi \varphi })\right]&{\hat {\mathbf {r} }}\\+\left[{\frac {\partial T_{r\theta }}{\partial r}}+2{\frac {T_{r\theta }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \theta }}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta \theta }+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \theta }}{\partial \varphi }}+{\frac {T_{\theta r}}{r}}-{\frac {\cot \theta }{r}}T_{\varphi \varphi }\right]&{\hat {\boldsymbol {\theta }}}\\+\left[{\frac {\partial T_{r\varphi }}{\partial r}}+2{\frac {T_{r\varphi }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \varphi }}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {T_{\varphi r}}{r}}+{\frac {\cot \theta }{r}}(T_{\theta \varphi }+T_{\varphi \theta })\right]&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}
Differential displacement dℓ [1] d x x ^ + d y y ^ + d z z ^ {\displaystyle dx\,{\hat {\mathbf {x} }}+dy\,{\hat {\mathbf {y} }}+dz\,{\hat {\mathbf {z} }}} d ρ ρ ^ + ρ d φ φ ^ + d z z ^ {\displaystyle d\rho \,{\hat {\boldsymbol {\rho }}}+\rho \,d\varphi \,{\hat {\boldsymbol {\varphi }}}+dz\,{\hat {\mathbf {z} }}} d r r ^ + r d θ θ ^ + r sin θ d φ φ ^ {\displaystyle dr\,{\hat {\mathbf {r} }}+r\,d\theta \,{\hat {\boldsymbol {\theta }}}+r\,\sin \theta \,d\varphi \,{\hat {\boldsymbol {\varphi }}}} Differential normal area d S d y d z x ^ + d x d z y ^ + d x d y z ^ {\displaystyle {\begin{aligned}dy\,dz&\,{\hat {\mathbf {x} }}\\{}+dx\,dz&\,{\hat {\mathbf {y} }}\\{}+dx\,dy&\,{\hat {\mathbf {z} }}\end{aligned}}} ρ d φ d z ρ ^ + d ρ d z φ ^ + ρ d ρ d φ z ^ {\displaystyle {\begin{aligned}\rho \,d\varphi \,dz&\,{\hat {\boldsymbol {\rho }}}\\{}+d\rho \,dz&\,{\hat {\boldsymbol {\varphi }}}\\{}+\rho \,d\rho \,d\varphi &\,{\hat {\mathbf {z} }}\end{aligned}}} r 2 sin θ d θ d φ r ^ + r sin θ d r d φ θ ^ + r d r d θ φ ^ {\displaystyle {\begin{aligned}r^{2}\sin \theta \,d\theta \,d\varphi &\,{\hat {\mathbf {r} }}\\{}+r\sin \theta \,dr\,d\varphi &\,{\hat {\boldsymbol {\theta }}}\\{}+r\,dr\,d\theta &\,{\hat {\boldsymbol {\varphi }}}\end{aligned}}} Differential volume dV [1] d x d y d z {\displaystyle dx\,dy\,dz} ρ d ρ d φ d z {\displaystyle \rho \,d\rho \,d\varphi \,dz} r 2 sin θ d r d θ d φ {\displaystyle r^{2}\sin \theta \,dr\,d\theta \,d\varphi }
^α θ {\displaystyle \theta } φ {\displaystyle \varphi } θ {\displaystyle \theta } φ {\displaystyle \varphi } θ {\displaystyle \theta } φ {\displaystyle \varphi } ^β ∂ i A ⊗ e i {\displaystyle \partial _{i}\mathbf {A} \otimes \mathbf {e} _{i}} e i ⊗ ∂ i A {\displaystyle \mathbf {e} _{i}\otimes \partial _{i}\mathbf {A} } ^γ e i ⋅ ∂ i T {\displaystyle \mathbf {e} _{i}\cdot \partial _{i}\mathbf {T} } ∂ i T ⋅ e i {\displaystyle \partial _{i}\mathbf {T} \cdot \mathbf {e} _{i}} Calculation rules div grad f ≡ ∇ ⋅ ∇ f ≡ ∇ 2 f {\displaystyle \operatorname {div} \,\operatorname {grad} f\equiv \nabla \cdot \nabla f\equiv \nabla ^{2}f} curl grad f ≡ ∇ × ∇ f = 0 {\displaystyle \operatorname {curl} \,\operatorname {grad} f\equiv \nabla \times \nabla f=\mathbf {0} } div curl A ≡ ∇ ⋅ ( ∇ × A ) = 0 {\displaystyle \operatorname {div} \,\operatorname {curl} \mathbf {A} \equiv \nabla \cdot (\nabla \times \mathbf {A} )=0} curl curl A ≡ ∇ × ( ∇ × A ) = ∇ ( ∇ ⋅ A ) − ∇ 2 A {\displaystyle \operatorname {curl} \,\operatorname {curl} \mathbf {A} \equiv \nabla \times (\nabla \times \mathbf {A} )=\nabla (\nabla \cdot \mathbf {A} )-\nabla ^{2}\mathbf {A} } Lagrange's formula for del)∇ 2 ( f g ) = f ∇ 2 g + 2 ∇ f ⋅ ∇ g + g ∇ 2 f {\displaystyle \nabla ^{2}(fg)=f\nabla ^{2}g+2\nabla f\cdot \nabla g+g\nabla ^{2}f} ∇ 2 ( P ⋅ Q ) = Q ⋅ ∇ 2 P − P ⋅ ∇ 2 Q + 2 ∇ ⋅ [ ( P ⋅ ∇ ) Q + P × ∇ × Q ] {\displaystyle \nabla ^{2}\left(\mathbf {P} \cdot \mathbf {Q} \right)=\mathbf {Q} \cdot \nabla ^{2}\mathbf {P} -\mathbf {P} \cdot \nabla ^{2}\mathbf {Q} +2\nabla \cdot \left[\left(\mathbf {P} \cdot \nabla \right)\mathbf {Q} +\mathbf {P} \times \nabla \times \mathbf {Q} \right]\quad } [4] )Cartesian derivation
div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A x ( x + d x ) d y d z − A x ( x ) d y d z + A y ( y + d y ) d x d z − A y ( y ) d x d z + A z ( z + d z ) d x d y − A z ( z ) d x d y d x d y d z = ∂ A x ∂ x + ∂ A y ∂ y + ∂ A z ∂ z {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} =\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}&={\frac {A_{x}(x+dx)\,dy\,dz-A_{x}(x)\,dy\,dz+A_{y}(y+dy)\,dx\,dz-A_{y}(y)\,dx\,dz+A_{z}(z+dz)\,dx\,dy-A_{z}(z)\,dx\,dy}{dx\,dy\,dz}}\\&={\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}
( curl A ) x = lim S ⊥ x ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A z ( y + d y ) d z − A z ( y ) d z + A y ( z ) d y − A y ( z + d z ) d y d y d z = ∂ A z ∂ y − ∂ A y ∂ z {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{x}=\lim _{S^{\perp \mathbf {\hat {x}} }\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{z}(y+dy)\,dz-A_{z}(y)\,dz+A_{y}(z)\,dy-A_{y}(z+dz)\,dy}{dy\,dz}}\\&={\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\end{aligned}}}
The expressions for ( curl A ) y {\displaystyle (\operatorname {curl} \mathbf {A} )_{y}} ( curl A ) z {\displaystyle (\operatorname {curl} \mathbf {A} )_{z}}
Cylindrical derivation
div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A ρ ( ρ + d ρ ) ( ρ + d ρ ) d ϕ d z − A ρ ( ρ ) ρ d ϕ d z + A ϕ ( ϕ + d ϕ ) d ρ d z − A ϕ ( ϕ ) d ρ d z + A z ( z + d z ) d ρ ( ρ + d ρ / 2 ) d ϕ − A z ( z ) d ρ ( ρ + d ρ / 2 ) d ϕ ρ d ϕ d ρ d z = 1 ρ ∂ ( ρ A ρ ) ∂ ρ + 1 ρ ∂ A ϕ ∂ ϕ + ∂ A z ∂ z {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{\rho }(\rho +d\rho )(\rho +d\rho )\,d\phi \,dz-A_{\rho }(\rho )\rho \,d\phi \,dz+A_{\phi }(\phi +d\phi )\,d\rho \,dz-A_{\phi }(\phi )\,d\rho \,dz+A_{z}(z+dz)\,d\rho \,(\rho +d\rho /2)\,d\phi -A_{z}(z)\,d\rho (\rho +d\rho /2)\,d\phi }{\rho \,d\phi \,d\rho \,dz}}\\&={\frac {1}{\rho }}{\frac {\partial (\rho A_{\rho })}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial A_{\phi }}{\partial \phi }}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}
( curl A ) ρ = lim S ⊥ ρ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ϕ ( z ) ( ρ + d ρ ) d ϕ − A ϕ ( z + d z ) ( ρ + d ρ ) d ϕ + A z ( ϕ + d ϕ ) d z − A z ( ϕ ) d z ( ρ + d ρ ) d ϕ d z = − ∂ A ϕ ∂ z + 1 ρ ∂ A z ∂ ϕ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\rho }&=\lim _{S^{\perp {\hat {\boldsymbol {\rho }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\[1ex]&={\frac {A_{\phi }(z)\left(\rho +d\rho \right)\,d\phi -A_{\phi }(z+dz)\left(\rho +d\rho \right)\,d\phi +A_{z}(\phi +d\phi )\,dz-A_{z}(\phi )\,dz}{\left(\rho +d\rho \right)\,d\phi \,dz}}\\[1ex]&=-{\frac {\partial A_{\phi }}{\partial z}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}\end{aligned}}}
( curl A ) ϕ = lim S ⊥ ϕ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A z ( ρ ) d z − A z ( ρ + d ρ ) d z + A ρ ( z + d z ) d ρ − A ρ ( z ) d ρ d ρ d z = − ∂ A z ∂ ρ + ∂ A ρ ∂ z {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }&=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\&={\frac {A_{z}(\rho )\,dz-A_{z}(\rho +d\rho )\,dz+A_{\rho }(z+dz)\,d\rho -A_{\rho }(z)\,d\rho }{d\rho \,dz}}\\&=-{\frac {\partial A_{z}}{\partial \rho }}+{\frac {\partial A_{\rho }}{\partial z}}\end{aligned}}}
( curl A ) z = lim S ⊥ z ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ρ ( ϕ ) d ρ − A ρ ( ϕ + d ϕ ) d ρ + A ϕ ( ρ + d ρ ) ( ρ + d ρ ) d ϕ − A ϕ ( ρ ) ρ d ϕ ρ d ρ d ϕ = − 1 ρ ∂ A ρ ∂ ϕ + 1 ρ ∂ ( ρ A ϕ ) ∂ ρ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{z}&=\lim _{S^{\perp {\hat {\boldsymbol {z}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}\\[1ex]&={\frac {A_{\rho }(\phi )\,d\rho -A_{\rho }(\phi +d\phi )\,d\rho +A_{\phi }(\rho +d\rho )(\rho +d\rho )\,d\phi -A_{\phi }(\rho )\rho \,d\phi }{\rho \,d\rho \,d\phi }}\\[1ex]&=-{\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \phi }}+{\frac {1}{\rho }}{\frac {\partial (\rho A_{\phi })}{\partial \rho }}\end{aligned}}}
curl A = ( curl A ) ρ ρ ^ + ( curl A ) ϕ ϕ ^ + ( curl A ) z z ^ = ( 1 ρ ∂ A z ∂ ϕ − ∂ A ϕ ∂ z ) ρ ^ + ( ∂ A ρ ∂ z − ∂ A z ∂ ρ ) ϕ ^ + 1 ρ ( ∂ ( ρ A ϕ ) ∂ ρ − ∂ A ρ ∂ ϕ ) z ^ {\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{\rho }{\hat {\boldsymbol {\rho }}}+(\operatorname {curl} \mathbf {A} )_{\phi }{\hat {\boldsymbol {\phi }}}+(\operatorname {curl} \mathbf {A} )_{z}{\hat {\boldsymbol {z}}}\\[1ex]&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}-{\frac {\partial A_{\phi }}{\partial z}}\right){\hat {\boldsymbol {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\hat {\boldsymbol {\phi }}}+{\frac {1}{\rho }}\left({\frac {\partial (\rho A_{\phi })}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \phi }}\right){\hat {\boldsymbol {z}}}\end{aligned}}}
Spherical derivation div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A r ( r + d r ) ( r + d r ) d θ ( r + d r ) sin θ d ϕ − A r ( r ) r d θ r sin θ d ϕ + A θ ( θ + d θ ) sin ( θ + d θ ) r d r d ϕ − A θ ( θ ) sin ( θ ) r d r d ϕ + A ϕ ( ϕ + d ϕ ) r d r d θ − A ϕ ( ϕ ) r d r d θ d r r d θ r sin θ d ϕ = 1 r 2 ∂ ( r 2 A r ) ∂ r + 1 r sin θ ∂ ( A θ sin θ ) ∂ θ + 1 r sin θ ∂ A ϕ ∂ ϕ {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{r}(r+dr)(r+dr)\,d\theta \,(r+dr)\sin \theta \,d\phi -A_{r}(r)r\,d\theta \,r\sin \theta \,d\phi +A_{\theta }(\theta +d\theta )\sin(\theta +d\theta )r\,dr\,d\phi -A_{\theta }(\theta )\sin(\theta )r\,dr\,d\phi +A_{\phi }(\phi +d\phi )r\,dr\,d\theta -A_{\phi }(\phi )r\,dr\,d\theta }{dr\,r\,d\theta \,r\sin \theta \,d\phi }}\\&={\frac {1}{r^{2}}}{\frac {\partial (r^{2}A_{r})}{\partial r}}+{\frac {1}{r\sin \theta }}{\frac {\partial (A_{\theta }\sin \theta )}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial A_{\phi }}{\partial \phi }}\end{aligned}}}
( curl A ) r = lim S ⊥ r ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A θ ( ϕ ) r d θ + A ϕ ( θ + d θ ) r sin ( θ + d θ ) d ϕ − A θ ( ϕ + d ϕ ) r d θ − A ϕ ( θ ) r sin ( θ ) d ϕ r d θ r sin θ d ϕ = 1 r sin θ ∂ ( A ϕ sin θ ) ∂ θ − 1 r sin θ ∂ A θ ∂ ϕ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{r}=\lim _{S^{\perp {\boldsymbol {\hat {r}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\theta }(\phi )r\,d\theta +A_{\phi }(\theta +d\theta )r\sin(\theta +d\theta )\,d\phi -A_{\theta }(\phi +d\phi )r\,d\theta -A_{\phi }(\theta )r\sin(\theta )\,d\phi }{r\,d\theta \,r\sin \theta \,d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {1}{r\sin \theta }}{\frac {\partial A_{\theta }}{\partial \phi }}\end{aligned}}}
( curl A ) θ = lim S ⊥ θ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ϕ ( r ) r sin θ d ϕ + A r ( ϕ + d ϕ ) d r − A ϕ ( r + d r ) ( r + d r ) sin θ d ϕ − A r ( ϕ ) d r d r r sin θ d ϕ = 1 r sin θ ∂ A r ∂ ϕ − 1 r ∂ ( r A ϕ ) ∂ r {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\theta }=\lim _{S^{\perp {\boldsymbol {\hat {\theta }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\phi }(r)r\sin \theta \,d\phi +A_{r}(\phi +d\phi )\,dr-A_{\phi }(r+dr)(r+dr)\sin \theta \,d\phi -A_{r}(\phi )\,dr}{dr\,r\sin \theta \,d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {1}{r}}{\frac {\partial (rA_{\phi })}{\partial r}}\end{aligned}}}
( curl A ) ϕ = lim S ⊥ ϕ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A r ( θ ) d r + A θ ( r + d r ) ( r + d r ) d θ − A r ( θ + d θ ) d r − A θ ( r ) r d θ r d r d θ = 1 r ∂ ( r A θ ) ∂ r − 1 r ∂ A r ∂ θ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{r}(\theta )\,dr+A_{\theta }(r+dr)(r+dr)\,d\theta -A_{r}(\theta +d\theta )\,dr-A_{\theta }(r)r\,d\theta }{r\,dr\,d\theta }}\\&={\frac {1}{r}}{\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {1}{r}}{\frac {\partial A_{r}}{\partial \theta }}\end{aligned}}}
curl A = ( curl A ) r r ^ + ( curl A ) θ θ ^ + ( curl A ) ϕ ϕ ^ = 1 r sin θ ( ∂ ( A ϕ sin θ ) ∂ θ − ∂ A θ ∂ ϕ ) r ^ + 1 r ( 1 sin θ ∂ A r ∂ ϕ − ∂ ( r A ϕ ) ∂ r ) θ ^ + 1 r ( ∂ ( r A θ ) ∂ r − ∂ A r ∂ θ ) ϕ ^ {\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{r}\,{\hat {\boldsymbol {r}}}+(\operatorname {curl} \mathbf {A} )_{\theta }\,{\hat {\boldsymbol {\theta }}}+(\operatorname {curl} \mathbf {A} )_{\phi }\,{\hat {\boldsymbol {\phi }}}\\[1ex]&={\frac {1}{r\sin \theta }}\left({\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial \phi }}\right){\hat {\boldsymbol {r}}}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {\partial (rA_{\phi })}{\partial r}}\right){\hat {\boldsymbol {\theta }}}+{\frac {1}{r}}\left({\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {\partial A_{r}}{\partial \theta }}\right){\hat {\boldsymbol {\phi }}}\end{aligned}}}
Related Research Articles In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point.
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three numbers, : the radial distance of the radial line r connecting the point to the fixed point of origin ; the polar angle θ of the radial line r ; and the azimuthal angle φ of the radial line r .
In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as
The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
In fluid dynamics, potential flow or irrotational flow refers to a description of a fluid flow with no vorticity in it. Such a description typically arises in the limit of vanishing viscosity, i.e., for an inviscid fluid and with no vorticity present in the flow.
The vorticity equation of fluid dynamics describes the evolution of the vorticity ω
In mathematics, a unit vector in a normed vector space is a vector of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols Δf (p ) of a function f p f p f (p )
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller than any relevant dimension of the body; so that its geometry and the constitutive properties of the material at each point of space can be assumed to be unchanged by the deformation.
In fluid dynamics, Stokes' law is an empirical law for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a viscous fluid. It was derived by George Gabriel Stokes in 1851 by solving the Stokes flow limit for small Reynolds numbers of the Navier–Stokes equations.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed by prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a functional to a change in a function on which the functional depends.
Stokes flow , also named creeping flow or creeping motion , is a type of fluid flow where advective inertial forces are small compared with viscous forces. The Reynolds number is low, i.e.
The derivation of the Navier–Stokes equations as well as their application and formulation for different families of fluids, is an important exercise in fluid dynamics with applications in mechanical engineering, physics, chemistry, heat transfer, and electrical engineering. A proof explaining the properties and bounds of the equations, such as Navier–Stokes existence and smoothness, is one of the important unsolved problems in mathematics.
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.
In mathematics, vector spherical harmonics (VSH ) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.
In fluid dynamics, the Stokes stream function is used to describe the streamlines and flow velocity in a three-dimensional incompressible flow with axisymmetry. A surface with a constant value of the Stokes stream function encloses a streamtube, everywhere tangential to the flow velocity vectors. Further, the volume flux within this streamtube is constant, and all the streamlines of the flow are located on this surface. The velocity field associated with the Stokes stream function is solenoidal—it has zero divergence. This stream function is named in honor of George Gabriel Stokes.
The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical simulations.
In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.
Multipole radiation is a theoretical framework for the description of electromagnetic or gravitational radiation from time-dependent distributions of distant sources. These tools are applied to physical phenomena which occur at a variety of length scales - from gravitational waves due to galaxy collisions to gamma radiation resulting from nuclear decay. Multipole radiation is analyzed using similar multipole expansion techniques that describe fields from static sources, however there are important differences in the details of the analysis because multipole radiation fields behave quite differently from static fields. This article is primarily concerned with electromagnetic multipole radiation, although the treatment of gravitational waves is similar.
References This page is based on this
Wikipedia article Text is available under the
CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.
