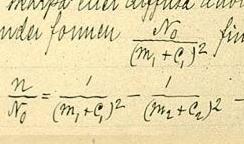In atomic theory and quantum mechanics, an atomic orbital is a function describing the location and wave-like behavior of an electron in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus. The term atomic orbital may also refer to the physical region or space where the electron can be calculated to be present, as predicted by the particular mathematical form of the orbital.
In atomic physics, the Bohr model or Rutherford–Bohr model of the atom, presented by Niels Bohr and Ernest Rutherford in 1913, consists of a small, dense nucleus surrounded by orbiting electrons. It is analogous to the structure of the Solar System, but with attraction provided by electrostatic force rather than gravity. In the history of atomic physics, it followed, and ultimately replaced, several earlier models, including Joseph Larmor's solar system model (1897), Jean Perrin's model (1901), the cubical model (1902), Hantaro Nagaoka's Saturnian model (1904), the plum pudding model (1904), Arthur Haas's quantum model (1910), the Rutherford model (1911), and John William Nicholson's nuclear quantum model (1912). The improvement over the 1911 Rutherford model mainly concerned the new quantum mechanical interpretation introduced by Haas and Nicholson, but forsaking any attempt to explain radiation according to classical physics.
In spectroscopy, the Rydberg constant, symbol for heavy atoms or for hydrogen, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to the electromagnetic spectra of an atom. The constant first arose as an empirical fitting parameter in the Rydberg formula for the hydrogen spectral series, but Niels Bohr later showed that its value could be calculated from more fundamental constants according to his model of the atom.
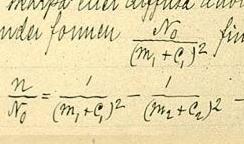
In atomic physics, the Rydberg formula calculates the wavelengths of a spectral line in many chemical elements. The formula was primarily presented as a generalization of the Balmer series for all atomic electron transitions of hydrogen. It was first empirically stated in 1888 by the Swedish physicist Johannes Rydberg, then theoretically by Niels Bohr in 1913, who used a primitive form of quantum mechanics. The formula directly generalizes the equations used to calculate the wavelengths of the hydrogen spectral series.
The Balmer series, or Balmer lines in atomic physics, is one of a set of six named series describing the spectral line emissions of the hydrogen atom. The Balmer series is calculated using the Balmer formula, an empirical equation discovered by Johann Balmer in 1885.
In physics and chemistry, the Lyman series is a hydrogen spectral series of transitions and resulting ultraviolet emission lines of the hydrogen atom as an electron goes from n ≥ 2 to n = 1, the lowest energy level of the electron. The transitions are named sequentially by Greek letters: from n = 2 to n = 1 is called Lyman-alpha, 3 to 1 is Lyman-beta, 4 to 1 is Lyman-gamma, and so on. The series is named after its discoverer, Theodore Lyman. The greater the difference in the principal quantum numbers, the higher the energy of the electromagnetic emission.
In atomic physics, a term symbol is an abbreviated description of the total spin and orbital angular momentum quantum numbers of the electrons in a multi-electron atom. So while the word symbol suggests otherwise, is represents an actual value of a physical quantity.
A Rydberg atom is an excited atom with one or more electrons that have a very high principal quantum number, n. The higher the value of n, the farther the electron is from the nucleus, on average. Rydberg atoms have a number of peculiar properties including an exaggerated response to electric and magnetic fields, long decay periods and electron wavefunctions that approximate, under some conditions, classical orbits of electrons about the nuclei. The core electrons shield the outer electron from the electric field of the nucleus such that, from a distance, the electric potential looks identical to that experienced by the electron in a hydrogen atom.
The aufbau principle, also called the aufbau rule, states that in the ground state of an atom or ion, electrons fill subshells of the lowest available energy, then they fill subshells of higher energy. For example, the 1s subshell is filled before the 2s subshell is occupied. In this way, the electrons of an atom or ion form the most stable electron configuration possible. An example is the configuration 1s2 2s2 2p6 3s2 3p3 for the phosphorus atom, meaning that the 1s subshell has 2 electrons, and so on.
The trihydrogen cation or protonated molecular hydrogen is a cation with formula H+
3, consisting of three hydrogen nuclei (protons) sharing two electrons.
The emission spectrum of atomic hydrogen has been divided into a number of spectral series, with wavelengths given by the Rydberg formula. These observed spectral lines are due to the electron making transitions between two energy levels in an atom. The classification of the series by the Rydberg formula was important in the development of quantum mechanics. The spectral series are important in astronomical spectroscopy for detecting the presence of hydrogen and calculating red shifts.
The Rydberg–Ritz combination principle is an empirical rule proposed by Walther Ritz in 1908 to describe the relationship of the spectral lines for all atoms, as a generalization of an earlier rule by Johannes Rydberg for the hydrogen atom and the alkali metals. The principle states that the spectral lines of any element include frequencies that are either the sum or the difference of the frequencies of two other lines. Lines of the spectra of elements could be predicted from existing lines. Since the frequency of light is proportional to the wavenumber or reciprocal wavelength, the principle can also be expressed in terms of wavenumbers which are the sum or difference of wavenumbers of two other lines.
The Rydberg states of an atom or molecule are electronically excited states with energies that follow the Rydberg formula as they converge on an ionic state with an ionization energy. Although the Rydberg formula was developed to describe atomic energy levels, it has been used to describe many other systems that have electronic structure roughly similar to atomic hydrogen. In general, at sufficiently high principal quantum numbers, an excited electron-ionic core system will have the general character of a hydrogenic system and the energy levels will follow the Rydberg formula. Rydberg states have energies converging on the energy of the ion. The ionization energy threshold is the energy required to completely liberate an electron from the ionic core of an atom or molecule. In practice, a Rydberg wave packet is created by a laser pulse on a hydrogenic atom and thus populates a superposition of Rydberg states. Modern investigations using pump-probe experiments show molecular pathways – e.g. dissociation of (NO)2 – via these special states.
The Inglis–Teller equation represents an approximate relationship between the plasma density and the principal quantum number of the highest bound state of an atom. The equation was derived by David R. Inglis and Edward Teller in 1939.
Imidogen is an inorganic compound with the chemical formula NH. Like other simple radicals, it is highly reactive and consequently short-lived except as a dilute gas. Its behavior depends on its spin multiplicity.
The Pickering series (also known as the Pickering–Fowler series) consists of three lines of singly ionized helium found, usually in absorption, in the spectra of hot stars like Wolf–Rayet stars. The name comes from Edward Charles Pickering and Alfred Fowler. The lines are produced by transitions from a higher energy level of an electron to a level with principal quantum number n = 4. The lines have wavelengths:
Modern spectroscopy in the Western world started in the 17th century. New designs in optics, specifically prisms, enabled systematic observations of the solar spectrum. Isaac Newton first applied the word spectrum to describe the rainbow of colors that combine to form white light. During the early 1800s, Joseph von Fraunhofer conducted experiments with dispersive spectrometers that enabled spectroscopy to become a more precise and quantitative scientific technique. Since then, spectroscopy has played and continues to play a significant role in chemistry, physics and astronomy. Fraunhofer observed and measured dark lines in the Sun's spectrum, which now bear his name although several of them were observed earlier by Wollaston.
The sharp series is a series of spectral lines in the atomic emission spectrum caused when electrons descend from higher-energy s orbitals of an atom to the lowest available p orbital. The spectral lines include some in the visible light, and they extend into the ultraviolet. The lines get closer and closer together as the frequency increases never exceeding the series limit. The sharp series was important in the development of the understanding of electron shells and subshells in atoms. The sharp series has given the letter s to the s atomic orbital or subshell.
The fundamental series is a set of spectral lines in a set caused by transition between d and f orbitals in atoms.
In atomic emission spectroscopy, the principal series is a series of spectral lines caused when electrons move between p orbitals of an atom and the lowest available s orbital. These lines are usually found in the visible and ultraviolet portions of the electromagnetic spectrum. The principal series has given the letter p to the p atomic orbital and subshell.
