
Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, D. Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation.

In mathematics, the error function, often denoted by erf, is a function defined as:

The Fresnel integralsS(x) and C(x) are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function (erf). They arise in the description of near-field Fresnel diffraction phenomena and are defined through the following integral representations:
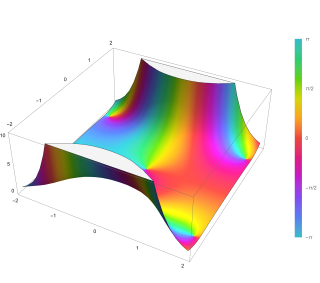
In mathematics, the Dawson function or Dawson integral (named after H. G. Dawson) is the one-sided Fourier–Laplace sine transform of the Gaussian function.

In electrochemistry, cyclic voltammetry (CV) is a type of potentiodynamic measurement. In a cyclic voltammetry experiment, the working electrode potential is ramped linearly versus time. Unlike in linear sweep voltammetry, after the set potential is reached in a CV experiment, the working electrode's potential is ramped in the opposite direction to return to the initial potential. These cycles of ramps in potential may be repeated as many times as needed. The current at the working electrode is plotted versus the applied voltage to give the cyclic voltammogram trace. Cyclic voltammetry is generally used to study the electrochemical properties of an analyte in solution or of a molecule that is adsorbed onto the electrode.

Voltammetry is a category of electroanalytical methods used in analytical chemistry and various industrial processes. In voltammetry, information about an analyte is obtained by measuring the current as the potential is varied. The analytical data for a voltammetric experiment comes in the form of a voltammogram, which plots the current produced by the analyte versus the potential of the working electrode.
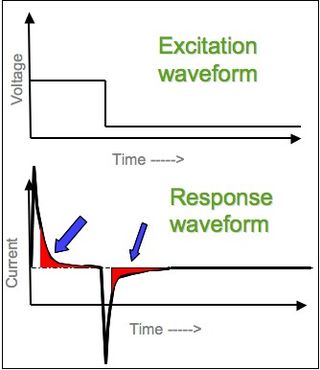
In electrochemistry, chronoamperometry is an analytical technique in which the electric potential of the working electrode is stepped and the resulting current from faradaic processes occurring at the electrode is monitored as a function of time. The functional relationship between current response and time is measured after applying single or double potential step to the working electrode of the electrochemical system. Limited information about the identity of the electrolyzed species can be obtained from the ratio of the peak oxidation current versus the peak reduction current. However, as with all pulsed techniques, chronoamperometry generates high charging currents, which decay exponentially with time as any RC circuit. The Faradaic current - which is due to electron transfer events and is most often the current component of interest - decays as described in the Cottrell equation. In most electrochemical cells, this decay is much slower than the charging decay-cells with no supporting electrolyte are notable exceptions. Most commonly a three-electrode system is used. Since the current is integrated over relatively longer time intervals, chronoamperometry gives a better signal-to-noise ratio in comparison to other amperometric techniques.
The Deal–Grove model mathematically describes the growth of an oxide layer on the surface of a material. In particular, it is used to predict and interpret thermal oxidation of silicon in semiconductor device fabrication. The model was first published in 1965 by Bruce Deal and Andrew Grove of Fairchild Semiconductor, building on Mohamed M. Atalla's work on silicon surface passivation by thermal oxidation at Bell Labs in the late 1950s. This served as a step in the development of CMOS devices and the fabrication of integrated circuits.

In electrochemistry, the Cottrell equation describes the change in electric current with respect to time in a controlled potential experiment, such as chronoamperometry. Specifically it describes the current response when the potential is a step function in time. It was derived by Frederick Gardner Cottrell in 1903. For a simple redox event, such as the ferrocene/ferrocenium couple, the current measured depends on the rate at which the analyte diffuses to the electrode. That is, the current is said to be "diffusion controlled". The Cottrell equation describes the case for an electrode that is planar but can also be derived for spherical, cylindrical, and rectangular geometries by using the corresponding Laplace operator and boundary conditions in conjunction with Fick's second law of diffusion.
In chemical analysis, matrix refers to the components of a sample other than the analyte of interest. The matrix can have a considerable effect on the way the analysis is conducted and the quality of the results are obtained; such effects are called matrix effects. For example, the ionic strength of the solution can have an effect on the activity coefficients of the analytes. The most common approach for accounting for matrix effects is to build a calibration curve using standard samples with known analyte concentration and which try to approximate the matrix of the sample as much as possible. This is especially important for solid samples where there is a strong matrix influence. In cases with complex or unknown matrices, the standard addition method can be used. In this technique, the response of the sample is measured and recorded, for example, using an electrode selective for the analyte. Then, a small volume of standard solution is added and the response is measured again. Ideally, the standard addition should increase the analyte concentration by a factor of 1.5 to 3, and several additions should be averaged. The volume of standard solution should be small enough to disturb the matrix as little as possible.
In analytical chemistry, a rotating disk electrode (RDE) is a working electrode used in three-electrode systems for hydrodynamic voltammetry. The electrode rotates during experiments, inducing a flux of analyte to the electrode. These working electrodes are used in electrochemical studies when investigating reaction mechanisms related to redox chemistry, among other chemical phenomena. The more complex rotating ring-disk electrode can be used as a rotating disk electrode if the ring is left inactive during the experiment.
More colloquially, a first passage time in a stochastic system, is the time taken for a state variable to reach a certain value. Understanding this metric allows one to further understand the physical system under observation, and as such has been the topic of research in very diverse fields, from economics to ecology.
In a body submerged in a fluid, unsteady forces due to acceleration of that body with respect to the fluid, can be divided into two parts: the virtual mass effect and the Basset force.

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing.
In electrochemistry, the Randles–Ševčík equation describes the effect of scan rate on the peak current for a cyclic voltammetry experiment. For simple redox events where the reaction is electrochemically reversible, and the products and reactants are both soluble, such as the ferrocene/ferrocenium couple, ip depends not only on the concentration and diffusional properties of the electroactive species but also on scan rate.
Liberation is the first step in the process by which medication enters the body and liberates the active ingredient that has been administered. The pharmaceutical drug must separate from the vehicle or the excipient that it was mixed with during manufacture. Some authors split the process of liberation into three steps: disintegration, disaggregation and dissolution. A limiting factor in the adsorption of pharmaceutical drugs is the degree to which they are ionized, as cell membranes are relatively impermeable to ionized molecules.
In electrochemistry, protein film voltammetry is a technique for examining the behavior of proteins immobilized on an electrode. The technique is applicable to proteins and enzymes that engage in electron transfer reactions and it is part of the methods available to study enzyme kinetics.
In mathematics, the exponential response formula (ERF), also known as exponential response and complex replacement, is a method used to find a particular solution of a non-homogeneous linear ordinary differential equation of any order. The exponential response formula is applicable to non-homogeneous linear ordinary differential equations with constant coefficients if the function is polynomial, sinusoidal, exponential or the combination of the three. The general solution of a non-homogeneous linear ordinary differential equation is a superposition of the general solution of the associated homogeneous ODE and a particular solution to the non-homogeneous ODE. Alternative methods for solving ordinary differential equations of higher order are method of undetermined coefficients and method of variation of parameters.

The Kaniadakis Gaussian distribution is a probability distribution which arises as a generalization of the Gaussian distribution from the maximization of the Kaniadakis entropy under appropriated constraints. It is one example of a Kaniadakis κ-distribution. The κ-Gaussian distribution has been applied successfully for describing several complex systems in economy, geophysics, astrophysics, among many others.
In electrochemistry, the Berzins-Delahay equation is analogous to the Randles–Sevcik equation, except that it predicts the peak height of a linear potential scan when the reaction is electrochemically reversible, the reactants are soluble, and the products are deposited on the electrode with a thermodynamic activity of one.














