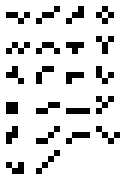Derived from the Greek word for '5', and "domino", a pentomino is a polyomino of order 5; that is, a polygon in the plane made of 5 equal-sized squares connected edge to edge. When rotations and reflections are not considered to be distinct shapes, there are 12 different free pentominoes. When reflections are considered distinct, there are 18 one-sided pentominoes. When rotations are also considered distinct, there are 63 fixed pentominoes.

A tetromino is a geometric shape composed of four squares, connected orthogonally. Tetrominoes, like dominoes and pentominoes, are a particular type of polyomino. The corresponding polycube, called a tetracube, is a geometric shape composed of four cubes connected orthogonally.

In Euclidean plane geometry, a rectangle is a rectilinear convex polygon or a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.

A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling.
A polyiamond is a polyform whose base form is an equilateral triangle. The word polyiamond is a back-formation from diamond, because this word is often used to describe the shape of a pair of equilateral triangles placed base to base, and the initial 'di-' looks like a Greek prefix meaning 'two-'. The name was suggested by recreational mathematics writer Thomas H. O'Beirne in New Scientist 1961 number 1, page 164.

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.

A hexomino is a polyomino of order 6; that is, a polygon in the plane made of 6 equal-sized squares connected edge to edge. The name of this type of figure is formed with the prefix hex(a)-. When rotations and reflections are not considered to be distinct shapes, there are 35 different free hexominoes. When reflections are considered distinct, there are 60 one-sided hexominoes. When rotations are also considered distinct, there are 216 fixed hexominoes.

In recreational mathematics, a polyabolo is a shape formed by gluing isosceles right triangles edge-to-edge, making a polyform with the isosceles right triangle as the base form. Polyaboloes were introduced by Martin Gardner in his June 1967 "Mathematical Games column" in Scientific American.

In recreational mathematics, a polyhex is a polyform with a regular hexagon as the base form, constructed by joining together 1 or more hexagons. Specific forms are named by their number of hexagons: monohex, dihex, trihex, tetrahex, etc. They were named by David Klarner who investigated them.

A polycube is a solid figure formed by joining one or more equal cubes face to face. Polycubes are the three-dimensional analogues of the planar polyominoes. The Soma cube, the Bedlam cube, the Diabolical cube, the Slothouber–Graatsma puzzle, and the Conway puzzle are examples of packing problems based on polycubes.

A tromino or triomino is a polyomino of size 3, that is, a polygon in the plane made of three equal-sized squares connected edge-to-edge.

A heptomino is a polyomino of order 7; that is, a polygon in the plane made of 7 equal-sized squares connected edge to edge. The name of this type of figure is formed with the prefix hept(a)-. When rotations and reflections are not considered to be distinct shapes, there are 108 different free heptominoes. When reflections are considered distinct, there are 196 one-sided heptominoes. When rotations are also considered distinct, there are 760 fixed heptominoes.

A nonomino is a polyomino of order 9; that is, a polygon in the plane made of 9 equal-sized squares connected edge to edge. The name of this type of figure is formed with the prefix non(a)-. When rotations and reflections are not considered to be distinct shapes, there are 1,285 different free nonominoes. When reflections are considered distinct, there are 2,500 one-sided nonominoes. When rotations are also considered distinct, there are 9,910 fixed nonominoes.

An octomino is a polyomino of order 8; that is, a polygon in the plane made of 8 equal-sized squares connected edge to edge. When rotations and reflections are not considered to be distinct shapes, there are 369 different free octominoes. When reflections are considered distinct, there are 704 one-sided octominoes. When rotations are also considered distinct, there are 2,725 fixed octominoes.

The mutilated chessboard problem is a tiling puzzle posed by Max Black in 1946 that asks:
Suppose a standard 8×8 chessboard has two diagonally opposite corners removed, leaving 62 squares. Is it possible to place 31 dominoes of size 2×1 so as to cover all of these squares?

In geometry, a domino tiling of a region in the Euclidean plane is a tessellation of the region by dominoes, shapes formed by the union of two unit squares meeting edge-to-edge. Equivalently, it is a perfect matching in the grid graph formed by placing a vertex at the center of each square of the region and connecting two vertices when they correspond to adjacent squares.

A Penrose tiling is an example of an aperiodic tiling. Here, a tiling is a covering of the plane by non-overlapping polygons or other shapes, and a tiling is aperiodic if it does not contain arbitrarily large periodic regions or patches. However, despite their lack of translational symmetry, Penrose tilings may have both reflection symmetry and fivefold rotational symmetry. Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated them in the 1970s.
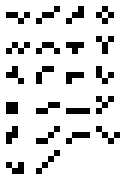
A pseudo-polyomino, also called a polyking, polyplet or hinged polyomino, is a plane geometric figure formed by joining one or more equal squares edge-to-edge or corner-to-corner at 90°. It is a polyform with square cells. The polyominoes are a subset of the polykings.
A decomino, or 10-omino, is a polyomino of order 10; that is, a polygon in the plane made of 10 equal-sized squares connected edge to edge. When rotations and reflections are not considered to be distinct shapes, there are 4,655 different free decominoes. When reflections are considered distinct, there are 9,189 one-sided decominoes. When rotations are also considered distinct, there are 36,446 fixed decominoes.

Polyominoes: Puzzles, Patterns, Problems, and Packings is a mathematics book on polyominoes, the shapes formed by connecting some number of unit squares edge-to-edge. It was written by Solomon Golomb, and is "universally regarded as a classic in recreational mathematics". The Basic Library List Committee of the Mathematical Association of America has strongly recommended its inclusion in undergraduate mathematics libraries.