
Derived from the Greek word for '5', and "domino", a pentomino is a polyomino of order 5; that is, a polygon in the plane made of 5 equal-sized squares connected edge to edge. When rotations and reflections are not considered to be distinct shapes, there are 12 different free pentominoes. When reflections are considered distinct, there are 18 one-sided pentominoes. When rotations are also considered distinct, there are 63 fixed pentominoes.

In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).

A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling.

In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.
A polyiamond is a polyform whose base form is an equilateral triangle. The word polyiamond is a back-formation from diamond, because this word is often used to describe the shape of a pair of equilateral triangles placed base to base, and the initial 'di-' looks like a Greek prefix meaning 'two-'. The name was suggested by recreational mathematics writer Thomas H. O'Beirne in New Scientist 1961 number 1, page 164.

A hexomino is a polyomino of order 6; that is, a polygon in the plane made of 6 equal-sized squares connected edge to edge. The name of this type of figure is formed with the prefix hex(a)-. When rotations and reflections are not considered to be distinct shapes, there are 35 different free hexominoes. When reflections are considered distinct, there are 60 one-sided hexominoes. When rotations are also considered distinct, there are 216 fixed hexominoes.

A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. For each wallpaper there corresponds a group of congruent transformations, with function composition as the group operation. Thus, a wallpaper group is a mathematical classification of a two‑dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tessellations, tiles and physical wallpaper.

Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.

In recreational mathematics, a polyhex is a polyform with a regular hexagon as the base form, constructed by joining together 1 or more hexagons. Specific forms are named by their number of hexagons: monohex, dihex, trihex, tetrahex, etc. They were named by David Klarner who investigated them.
The Schoenfliesnotation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the symmetry of a molecule, the notation is often sufficient and commonly used for spectroscopy. However, in crystallography, there is additional translational symmetry, and point groups are not enough to describe the full symmetry of crystals, so the full space group is usually used instead. The naming of full space groups usually follows another common convention, the Hermann–Mauguin notation, also known as the international notation.

A heptomino is a polyomino of order 7; that is, a polygon in the plane made of 7 equal-sized squares connected edge to edge. The name of this type of figure is formed with the prefix hept(a)-. When rotations and reflections are not considered to be distinct shapes, there are 108 different free heptominoes. When reflections are considered distinct, there are 196 one-sided heptominoes. When rotations are also considered distinct, there are 760 fixed heptominoes.

A nonomino is a polyomino of order 9; that is, a polygon in the plane made of 9 equal-sized squares connected edge to edge. The name of this type of figure is formed with the prefix non(a)-. When rotations and reflections are not considered to be distinct shapes, there are 1,285 different free nonominoes. When reflections are considered distinct, there are 2,500 one-sided nonominoes. When rotations are also considered distinct, there are 9,910 fixed nonominoes.

In mathematics, D3 (sometimes alternatively denoted by D6) is the dihedral group of degree 3 and order 6. It equals the symmetric group S3. It is also the smallest non-abelian group.
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.

A regular octahedron has 24 rotational symmetries, and 48 symmetries altogether. These include transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the polyhedron that is dual to an octahedron.
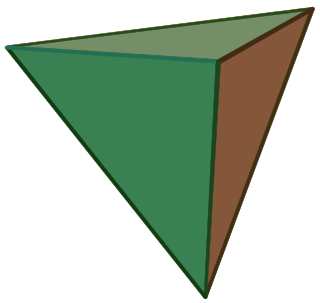
A regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dihn.

An octomino is a polyomino of order 8; that is, a polygon in the plane made of 8 equal-sized squares connected edge to edge. When rotations and reflections are not considered to be distinct shapes, there are 369 different free octominoes. When reflections are considered distinct, there are 704 one-sided octominoes. When rotations are also considered distinct, there are 2,725 fixed octominoes.
In mathematics, a symmetry operation is a geometric transformation of an object that leaves the object looking the same after it has been carried out. For example, a 1⁄3 turn rotation of a regular triangle about its center, a reflection of a square across its diagonal, a translation of the Euclidean plane, or a point reflection of a sphere through its center are all symmetry operations. Each symmetry operation is performed with respect to some symmetry element.

In chemistry, molecular symmetry describes the symmetry present in molecules and the classification of these molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can be used to predict or explain many of a molecule's chemical properties, such as whether or not it has a dipole moment, as well as its allowed spectroscopic transitions. To do this it is necessary to use group theory. This involves classifying the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Symmetry is useful in the study of molecular orbitals, with applications to the Hückel method, to ligand field theory, and to the Woodward-Hoffmann rules. Many university level textbooks on physical chemistry, quantum chemistry, spectroscopy and inorganic chemistry discuss symmetry. Another framework on a larger scale is the use of crystal systems to describe crystallographic symmetry in bulk materials.
















