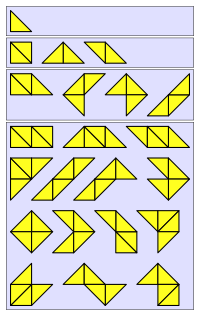
In recreational mathematics, a polyabolo (also known as a polytan) is a shape formed by gluing isosceles right triangles edge-to-edge, making a polyform with the isosceles right triangle as the base form. Polyaboloes were introduced by Martin Gardner in his June 1967 "Mathematical Games column" in Scientific American . [1]
The name polyabolo is a back formation from the juggling object 'diabolo', although the shape formed by joining two triangles at just one vertex is not a proper polyabolo. By false analogy, treating the di- in diabolo as meaning "two", polyaboloes with from 1 to 10 cells are called respectively monaboloes, diaboloes, triaboloes, tetraboloes, pentaboloes, hexaboloes, heptaboloes, octaboloes, enneaboloes, and decaboloes. The name polytan is derived from Henri Picciotto's name tetratan and alludes to the ancient Chinese amusement of tangrams.
There are two ways in which a square in a polyabolo can consist of two isosceles right triangles, but polyaboloes are considered equivalent if they have the same boundaries. The number of nonequivalent polyaboloes composed of 1, 2, 3, … triangles is 1, 3, 4, 14, 30, 107, 318, 1116, 3743, … (sequence A006074 in the OEIS ).
Polyaboloes that are confined strictly to the plane and cannot be turned over may be termed one-sided. The number of one-sided polyaboloes composed of 1, 2, 3, … triangles is 1, 4, 6, 22, 56, 198, 624, 2182, 7448, … (sequence A151519 in the OEIS ).
As for a polyomino, a polyabolo that can be neither turned over nor rotated may be termed fixed. A polyabolo with no symmetries (rotation or reflection) corresponds to 8 distinct fixed polyaboloes.
A non-simply connected polyabolo is one that has one or more holes in it. The smallest value of n for which an n-abolo is non-simply connected is 7.
In 1968, David A. Klarner defined the order of a polyomino. Similarly, the order of a polyabolo P can be defined as the minimum number of congruent copies of P that can be assembled (allowing translation, rotation, and reflection) to form a rectangle.
A polyabolo has order 1 if and only if it is itself a rectangle. Polyaboloes of order 2 are also easily recognisable. Solomon W. Golomb found polyaboloes, including a triabolo, of order 8. [2] Michael Reid found a heptabolo of order 6. [3] Higher orders are possible.
There are interesting tessellations of the Euclidean plane involving polyaboloes. One such is the tetrakis square tiling, a monohedral tessellation that fills the entire Euclidean plane with 45–45–90 triangles.
The Compatibility Problem is to take two or more polyaboloes and find a figure that can be tiled with each. This problem has been studied far less than the Compatibility Problem for polyominoes. Systematic results first appeared in 2004 at Erich Friedman's website Math Magic. [4]
Derived from the Greek word for '5', and "domino", a pentomino is a polyomino of order 5; that is, a polygon in the plane made of 5 equal-sized squares connected edge to edge. When rotations and reflections are not considered to be distinct shapes, there are 12 different free pentominoes. When reflections are considered distinct, there are 18 one-sided pentominoes. When rotations are also considered distinct, there are 63 fixed pentominoes.
In Euclidean plane geometry, a rectangle is a rectilinear convex polygon or a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling.
A polyiamond is a polyform whose base form is an equilateral triangle. The word polyiamond is a back-formation from diamond, because this word is often used to describe the shape of a pair of equilateral triangles placed base to base, and the initial 'di-' looks like a Greek prefix meaning 'two-'. The name was suggested by recreational mathematics writer Thomas H. O'Beirne in New Scientist 1961 number 1, page 164.
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.
A hexomino is a polyomino of order 6; that is, a polygon in the plane made of 6 equal-sized squares connected edge to edge. The name of this type of figure is formed with the prefix hex(a)-. When rotations and reflections are not considered to be distinct shapes, there are 35 different free hexominoes. When reflections are considered distinct, there are 60 one-sided hexominoes. When rotations are also considered distinct, there are 216 fixed hexominoes.
In recreational mathematics, a polyhex is a polyform with a regular hexagon as the base form, constructed by joining together 1 or more hexagons. Specific forms are named by their number of hexagons: monohex, dihex, trihex, tetrahex, etc. They were named by David Klarner who investigated them.
A tromino or triomino is a polyomino of size 3, that is, a polygon in the plane made of three equal-sized squares connected edge-to-edge.
Euclidean plane tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in his Harmonices Mundi.
A heptomino is a polyomino of order 7; that is, a polygon in the plane made of 7 equal-sized squares connected edge to edge. The name of this type of figure is formed with the prefix hept(a)-. When rotations and reflections are not considered to be distinct shapes, there are 108 different free heptominoes. When reflections are considered distinct, there are 196 one-sided heptominoes. When rotations are also considered distinct, there are 760 fixed heptominoes.
A nonomino is a polyomino of order 9; that is, a polygon in the plane made of 9 equal-sized squares connected edge to edge. The name of this type of figure is formed with the prefix non(a)-. When rotations and reflections are not considered to be distinct shapes, there are 1,285 different free nonominoes. When reflections are considered distinct, there are 2,500 one-sided nonominoes. When rotations are also considered distinct, there are 9,910 fixed nonominoes.
In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.
In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.
In geometry, the truncated square tiling is a semiregular tiling by regular polygons of the Euclidean plane with one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon. It has Schläfli symbol of t{4,4}.
In geometry, the rhombitrihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one triangle, two squares, and one hexagon on each vertex. It has Schläfli symbol of rr{3,6}.
An octomino is a polyomino of order 8; that is, a polygon in the plane made of 8 equal-sized squares connected edge to edge. When rotations and reflections are not considered to be distinct shapes, there are 369 different free octominoes. When reflections are considered distinct, there are 704 one-sided octominoes. When rotations are also considered distinct, there are 2,725 fixed octominoes.
In mathematics, a domino is a polyomino of order 2, that is, a polygon in the plane made of two equal-sized squares connected edge-to-edge. When rotations and reflections are not considered to be distinct shapes, there is only one free domino.
In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of Scientific American. In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in Mathematics Magazine.
In geometry, the rhombitrioctagonal tiling is a semiregular tiling of the hyperbolic plane. At each vertex of the tiling there is one triangle and one octagon, alternating between two squares. The tiling has Schläfli symbol rr{8,3}. It can be seen as constructed as a rectified trioctagonal tiling, r{8,3}, as well as an expanded octagonal tiling or expanded order-8 triangular tiling.
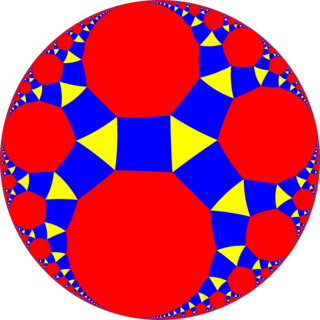
In geometry, the rhombtriapeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of rr{∞,3}.
| Polyominoes | |
|---|---|
| Higher dimensions | |
| Others | |
| Games and puzzles | |
