
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral hydrogen atom contains a nucleus of a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.
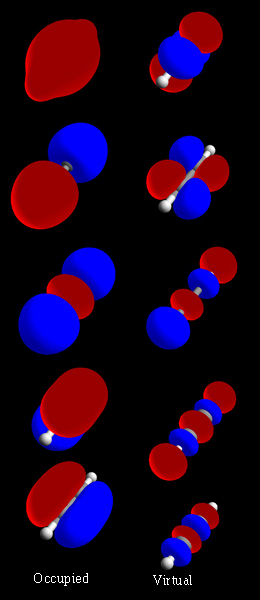
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The terms atomic orbital and molecular orbital were introduced by Robert S. Mulliken in 1932 to mean one-electron orbital wave functions. At an elementary level, they are used to describe the region of space in which a function has a significant amplitude.

Paramagnetism is a form of magnetism whereby some materials are weakly attracted by an externally applied magnetic field, and form internal, induced magnetic fields in the direction of the applied magnetic field. In contrast with this behavior, diamagnetic materials are repelled by magnetic fields and form induced magnetic fields in the direction opposite to that of the applied magnetic field. Paramagnetic materials include most chemical elements and some compounds; they have a relative magnetic permeability slightly greater than 1 and hence are attracted to magnetic fields. The magnetic moment induced by the applied field is linear in the field strength and rather weak. It typically requires a sensitive analytical balance to detect the effect and modern measurements on paramagnetic materials are often conducted with a SQUID magnetometer.

In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.

A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized.
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the best-known mathematical approximation in molecular dynamics. Specifically, it is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much heavier than the electrons. Due to the larger relative mass of a nucleus compared to an electron, the coordinates of the nuclei in a system are approximated as fixed, while the coordinates of the electrons are dynamic. The approach is named after Max Born and his 23-year-old graduate student J. Robert Oppenheimer, the latter of whom proposed it in 1927 during a period of intense ferment in the development of quantum mechanics.
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunctions. In a mathematical sense, these wave functions are the basis set of functions, the basis functions, which describe the electrons of a given atom. In chemical reactions, orbital wavefunctions are modified, i.e. the electron cloud shape is changed, according to the type of atoms participating in the chemical bond.

In atomic physics, hyperfine structure is defined by small shifts in otherwise degenerate electronic energy levels and the resulting splittings in those electronic energy levels of atoms, molecules, and ions, due to electromagnetic multipole interaction between the nucleus and electron clouds.

In quantum physics and chemistry, quantum numbers are quantities that characterize the possible states of the system. To fully specify the state of the electron in a hydrogen atom, four quantum numbers are needed. The traditional set of quantum numbers includes the principal, azimuthal, magnetic, and spin quantum numbers. To describe other systems, different quantum numbers are required. For subatomic particles, one needs to introduce new quantum numbers, such as the flavour of quarks, which have no classical correspondence.
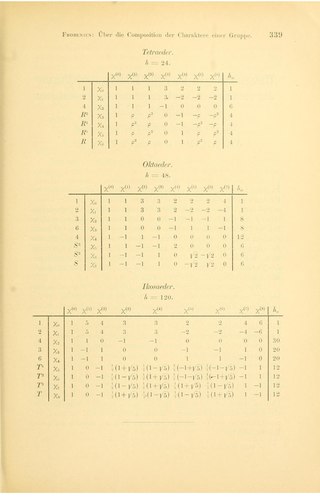
In group theory, a branch of abstract algebra, a character table is a two-dimensional table whose rows correspond to irreducible representations, and whose columns correspond to conjugacy classes of group elements. The entries consist of characters, the traces of the matrices representing group elements of the column's class in the given row's group representation. In chemistry, crystallography, and spectroscopy, character tables of point groups are used to classify e.g. molecular vibrations according to their symmetry, and to predict whether a transition between two states is forbidden for symmetry reasons. Many university level textbooks on physical chemistry, quantum chemistry, spectroscopy and inorganic chemistry devote a chapter to the use of symmetry group character tables.
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it can also refer to the simultaneous flip in the sign of all three spatial coordinates :
The Jahn–Teller effect is an important mechanism of spontaneous symmetry breaking in molecular and solid-state systems which has far-reaching consequences in different fields, and is responsible for a variety of phenomena in spectroscopy, stereochemistry, crystal chemistry, molecular and solid-state physics, and materials science. The effect is named for Hermann Arthur Jahn and Edward Teller, who first reported studies about it in 1937.
Multi-configurational self-consistent field (MCSCF) is a method in quantum chemistry used to generate qualitatively correct reference states of molecules in cases where Hartree–Fock and density functional theory are not adequate. It uses a linear combination of configuration state functions (CSF), or configuration determinants, to approximate the exact electronic wavefunction of an atom or molecule. In an MCSCF calculation, the set of coefficients of both the CSFs or determinants and the basis functions in the molecular orbitals are varied to obtain the total electronic wavefunction with the lowest possible energy. This method can be considered a combination between configuration interaction and Hartree–Fock.
Unrestricted Hartree–Fock (UHF) theory is the most common molecular orbital method for open shell molecules where the number of electrons of each spin are not equal. While restricted Hartree–Fock theory uses a single molecular orbital twice, one multiplied by the α spin function and the other multiplied by the β spin function in the Slater determinant, unrestricted Hartree–Fock theory uses different molecular orbitals for the α and β electrons. This has been called a different orbitals for different spins (DODS) method. The result is a pair of coupled Roothaan equations, known as the Pople–Nesbet–Berthier equations.
In computational chemistry, spin contamination is the artificial mixing of different electronic spin-states. This can occur when an approximate orbital-based wave function is represented in an unrestricted form – that is, when the spatial parts of α and β spin-orbitals are permitted to differ. Approximate wave functions with a high degree of spin contamination are undesirable. In particular, they are not eigenfunctions of the total spin-squared operator, Ŝ2, but can formally be expanded in terms of pure spin states of higher multiplicities.
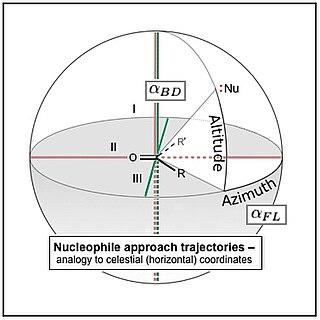
The Flippin–Lodge angle is one of two angles used by organic and biological chemists studying the relationship between a molecule's chemical structure and ways that it reacts, for reactions involving "attack" of an electron-rich reacting species, the nucleophile, on an electron-poor reacting species, the electrophile. Specifically, the angles—the Bürgi–Dunitz, , and the Flippin–Lodge, —describe the "trajectory" or "angle of attack" of the nucleophile as it approaches the electrophile, in particular when the latter is planar in shape. This is called a nucleophilic addition reaction and it plays a central role in the biological chemistry taking place in many biosyntheses in nature, and is a central "tool" in the reaction toolkit of modern organic chemistry, e.g., to construct new molecules such as pharmaceuticals. Theory and use of these angles falls into the areas of synthetic and physical organic chemistry, which deals with chemical structure and reaction mechanism, and within a sub-specialty called structure correlation.
In its most general form, the magnetoelectric effect (ME) denotes any coupling between the magnetic and the electric properties of a material. The first example of such an effect was described by Wilhelm Röntgen in 1888, who found that a dielectric material moving through an electric field would become magnetized. A material where such a coupling is intrinsically present is called a magnetoelectric.
Magnetochemistry is concerned with the magnetic properties of chemical compounds and elements. Magnetic properties arise from the spin and orbital angular momentum of the electrons contained in a compound. Compounds are diamagnetic when they contain no unpaired electrons. Molecular compounds that contain one or more unpaired electrons are paramagnetic. The magnitude of the paramagnetism is expressed as an effective magnetic moment, μeff. For first-row transition metals the magnitude of μeff is, to a first approximation, a simple function of the number of unpaired electrons, the spin-only formula. In general, spin–orbit coupling causes μeff to deviate from the spin-only formula. For the heavier transition metals, lanthanides and actinides, spin–orbit coupling cannot be ignored. Exchange interaction can occur in clusters and infinite lattices, resulting in ferromagnetism, antiferromagnetism or ferrimagnetism depending on the relative orientations of the individual spins.
Molecular symmetry in physics and chemistry describes the symmetry present in molecules and the classification of molecules according to their symmetry. Molecular symmetry is a fundamental concept in the application of Quantum Mechanics in physics and chemistry, for example it can be used to predict or explain many of a molecule's properties, such as its dipole moment and its allowed spectroscopic transitions, without doing the exact rigorous calculations. To do this it is necessary to classify the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Among all the molecular symmetries, diatomic molecules show some distinct features and they are relatively easier to analyze.
In applied mathematics, finite subgroups of SU(2) are groups composed of rotations and related transformations, employed particularly in the field of physical chemistry. The symmetry group of a physical body generally contains a subgroup of the 3D rotation group. It may occur that the group {±1} with two elements acts also on the body; this is typically the case in magnetism for the exchange of north and south poles, or in quantum mechanics for the change of spin sign. In this case, the symmetry group of a body may be a central extension of the group of spatial symmetries by the group with two elements. Hans Bethe introduced the term "double group" (Doppelgruppe) for such a group, in which two different elements induce the spatial identity, and a rotation of 2π may correspond to an element of the double group that is not the identity.








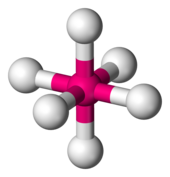
![Structure of a square-planar complex ion such as [AgF4] Square-planar-3D-balls.png](http://upload.wikimedia.org/wikipedia/commons/thumb/5/5b/Square-planar-3D-balls.png/170px-Square-planar-3D-balls.png)









