In mathematics, a recurrence relation is an equation that recursively defines a sequence or multidimensional array of values, once one or more initial terms are given; each further term of the sequence or array is defined as a function of the preceding terms.

In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It is named after Swedish mathematician Waloddi Weibull, who described it in detail in 1951, although it was first identified by Fréchet (1927) and first applied by Rosin & Rammler (1933) to describe a particle size distribution.

In economics and econometrics, the Cobb–Douglas production function is a particular functional form of the production function, widely used to represent the technological relationship between the amounts of two or more inputs and the amount of output that can be produced by those inputs. The Cobb–Douglas form was developed and tested against statistical evidence by Charles Cobb and Paul Douglas during 1927–1947.
In finance, arbitrage pricing theory (APT) is a general theory of asset pricing that holds that the expected return of a financial asset can be modeled as a linear function of various factors or theoretical market indices, where sensitivity to changes in each factor is represented by a factor-specific beta coefficient. The model-derived rate of return will then be used to price the asset correctly—the asset price should equal the expected end of period price discounted at the rate implied by the model. If the price diverges, arbitrage should bring it back into line. The theory was proposed by the economist Stephen Ross in 1976. The linear factor model structure of the APT is used as the basis for many of the commercial risk systems employed by asset managers.
The Hodrick–Prescott filter is a mathematical tool used in macroeconomics, especially in real business cycle theory, to remove the cyclical component of a time series from raw data. It is used to obtain a smoothed-curve representation of a time series, one that is more sensitive to long-term than to short-term fluctuations. The adjustment of the sensitivity of the trend to short-term fluctuations is achieved by modifying a multiplier . The filter was popularized in the field of economics in the 1990s by economists Robert J. Hodrick and Nobel Memorial Prize winner Edward C. Prescott. However, it was first proposed much earlier by E. T. Whittaker in 1923.
Trip distribution is the second component in the traditional four-step transportation forecasting model. This step matches tripmakers’ origins and destinations to develop a “trip table”, a matrix that displays the number of trips going from each origin to each destination. Historically, this component has been the least developed component of the transportation planning model.
In statistics, multicollinearity is a phenomenon in which one predictor variable in a multiple regression model can be linearly predicted from the others with a substantial degree of accuracy. In this situation the coefficient estimates of the multiple regression may change erratically in response to small changes in the model or the data. Multicollinearity does not reduce the predictive power or reliability of the model as a whole, at least within the sample data set; it only affects calculations regarding individual predictors. That is, a multivariate regression model with collinear predictors can indicate how well the entire bundle of predictors predicts the outcome variable, but it may not give valid results about any individual predictor, or about which predictors are redundant with respect to others.
In probability theory and statistics, a unit root is a feature of some stochastic processes that can cause problems in statistical inference involving time series models. A linear stochastic process has a unit root, if 1 is a root of the process's characteristic equation. Such a process is non-stationary but does not always have a trend.
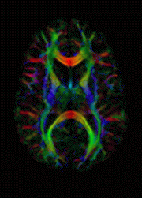
Diffusion-weighted magnetic resonance imaging is the use of specific MRI sequences as well as software that generates images from the resulting data that uses the diffusion of water molecules to generate contrast in MR images. It allows the mapping of the diffusion process of molecules, mainly water, in biological tissues, in vivo and non-invasively. Molecular diffusion in tissues is not free, but reflects interactions with many obstacles, such as macromolecules, fibers, and membranes. Water molecule diffusion patterns can therefore reveal microscopic details about tissue architecture, either normal or in a diseased state. A special kind of DWI, diffusion tensor imaging (DTI), has been used extensively to map white matter tractography in the brain.
Difference in differences is a statistical technique used in econometrics and quantitative research in the social sciences that attempts to mimic an experimental research design using observational study data, by studying the differential effect of a treatment on a 'treatment group' versus a 'control group' in a natural experiment. It calculates the effect of a treatment on an outcome by comparing the average change over time in the outcome variable for the treatment group, compared to the average change over time for the control group. Although it is intended to mitigate the effects of extraneous factors and selection bias, depending on how the treatment group is chosen, this method may still be subject to certain biases.

In statistics, a fixed effects model is a statistical model in which the model parameters are fixed or non-random quantities. This is in contrast to random effects models and mixed models in which all or some of the model parameters are considered as random variables. In many applications including econometrics and biostatistics a fixed effects model refers to a regression model in which the group means are fixed (non-random) as opposed to a random effects model in which the group means are a random sample from a population. Generally, data can be grouped according to several observed factors. The group means could be modeled as fixed or random effects for each grouping. In a fixed effects model each group mean is a group-specific fixed quantity.
The Hamiltonian is a function used to solve a problem of optimal control for a dynamical system. It can be understood as an instantaneous increment of the Lagrangian expression of the problem that is to be optimized over a certain time horizon. Inspired by, but distinct from, the Hamiltonian of classical mechanics, the Hamiltonian of optimal control theory was developed by Lev Pontryagin as part of his maximum principle. Pontryagin proved that a necessary condition for solving the optimal control problem is that the control should be chosen so as to optimize the Hamiltonian.
In actuarial science and applied probability ruin theory uses mathematical models to describe an insurer's vulnerability to insolvency/ruin. In such models key quantities of interest are the probability of ruin, distribution of surplus immediately prior to ruin and deficit at time of ruin.
In economics, the absolute income hypothesis concerns how a consumer divides his disposable income between consumption and saving. It is part of the theory of consumption proposed by English economist John Maynard Keynes (1883–1946). The hypothesis was refined extensively during the 1960s and 1970s, notably by American economist James Tobin (1918–2002).

In probability theory and statistics, the Poisson distribution, named after French mathematician Siméon Denis Poisson, is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event. The Poisson distribution can also be used for the number of events in other specified intervals such as distance, area or volume.
In macroeconomics, the cost of business cycles is the decrease in social welfare, if any, caused by business cycle fluctuations.
In the technological theory of social production, the growth of output, measured in money units, is related to achievements in technological consumption of labour and energy. This theory is based on concepts of classical political economy and neo-classical economics and appears to be a generalisation of the known economic models, such as the neo-classical model of economic growth and input-output model.
The Taylor contract or staggered contract was first formulated by John B. Taylor in his two articles, in 1979 "Staggered wage setting in a macro model'. and in 1980 "Aggregate Dynamics and Staggered Contracts". In its simplest form, one can think of two equal sized unions who set wages in an industry. Each period, one of the unions sets the nominal wage for two periods. This means that in any one period, only one of the unions can reset its wage and react to events that have just happened. When the union sets its wage, it sets it for a known and fixed period of time. Whilst it will know what is happening in the first period when it sets the new wage, it will have to form expectations about the factors in the second period that determine the optimal wage to set. Although the model was first used to model wage setting, in new Keynesian models that followed it was also used to model price-setting by firms.
In probability and statistics, the skewed generalized “t” distribution is a family of continuous probability distributions. The distribution was first introduced by Panayiotis Theodossiou in 1998. The distribution has since been used in different applications. There are different parameterizations for the skewed generalized t distribution.

The ISM Report On Business® (ROB), popularly known as the ISM Report, is the collective name for two monthly reports, the Manufacturing ISM Report On Business® and the Non-Manufacturing ISM Report On Business®, published by Institute for Supply Management. The ROB is based on a national survey of purchasing managers tracking changes in the manufacturing and non-manufacturing sectors. It is considered to be one of the most reliable economic barometers of the U.S. economy and gives an important early look at the health of the nation’s economy. In addition to being market moving, the ROB makes an important contribution to the American statistical system and to economic policy. It also has one of the shortest reporting lags of any macroeconomic series.












