
In geometry, the circumference is the perimeter of a circle or ellipse. The circumference is the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length around any closed figure. Circumference may also refer to the circle itself, that is, the locus corresponding to the edge of a disk. The circumference of a sphere is the circumference, or length, of any one of its great circles.
In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra.

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example,
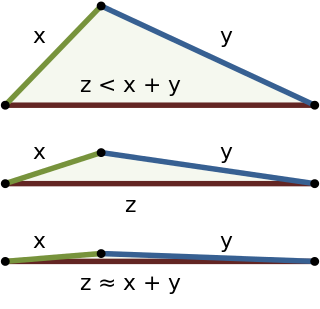
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If a, b, and c are the lengths of the sides of a triangle then the triangle inequality states that

In the mathematical field of differential geometry, the Gauss–Bonnet theorem is a fundamental formula which links the curvature of a surface to its underlying topology.

An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the special case of an isosceles triangle by modern definition, creating more special properties.

In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in -dimensional Euclidean space.

Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Many of these problems can be related to real-life packaging, storage and transportation issues. Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.

In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.
Distance geometry is the branch of mathematics concerned with characterizing and studying sets of points based only on given values of the distances between pairs of points. More abstractly, it is the study of semimetric spaces and the isometric transformations between them. In this view, it can be considered as a subject within general topology.

In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {5,3,3}. It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, hecatonicosachoron, dodecacontachoron and hecatonicosahedroid.

In mathematics, systolic geometry is the study of systolic invariants of manifolds and polyhedra, as initially conceived by Charles Loewner and developed by Mikhail Gromov, Michael Freedman, Peter Sarnak, Mikhail Katz, Larry Guth, and others, in its arithmetical, ergodic, and topological manifestations. See also Introduction to systolic geometry.

In geometry, Euler's theorem states that the distance d between the circumcenter and incenter of a triangle is given by or equivalently where and denote the circumradius and inradius respectively. The theorem is named for Leonhard Euler, who published it in 1765. However, the same result was published earlier by William Chapple in 1746.
In geometry, Jung's theorem is an inequality between the diameter of a set of points in any Euclidean space and the radius of the minimum enclosing ball of that set. It is named after Heinrich Jung, who first studied this inequality in 1901. Algorithms also exist to solve the smallest-circle problem explicitly.
In mathematics, a space, where is a real number, is a specific type of metric space. Intuitively, triangles in a space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature . In a space, the curvature is bounded from above by . A notable special case is ; complete spaces are known as "Hadamard spaces" after the French mathematician Jacques Hadamard.
In convex geometry, the Mahler volume of a centrally symmetric convex body is a dimensionless quantity that is associated with the body and is invariant under linear transformations. It is named after German-English mathematician Kurt Mahler. It is known that the shapes with the largest possible Mahler volume are the balls and solid ellipsoids; this is now known as the Blaschke–Santaló inequality. The still-unsolved Mahler conjecture states that the minimum possible Mahler volume is attained by a hypercube.
An acute triangle is a triangle with three acute angles. An obtuse triangle is a triangle with one obtuse angle and two acute angles. Since a triangle's angles must sum to 180° in Euclidean geometry, no Euclidean triangle can have more than one obtuse angle.
In geometry, it is an unsolved conjecture of Hugo Hadwiger that every simplex can be dissected into orthoschemes, using a number of orthoschemes bounded by a function of the dimension of the simplex. If true, then more generally every convex polytope could be dissected into orthoschemes.
William Chapple (1718–1781) was an English surveyor and mathematician. His mathematical discoveries were mostly in plane geometry and include:






























