 | This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these messages)
|
Egon Schulte (born January 7, 1955, in Heggen (Kreis Olpe), Germany) is a mathematician [1] and a professor of mathematics at Northeastern University in Boston. He received his Ph.D. in 1980 from the Technical University of Dortmund; his doctoral dissertation was on Regular Incidence Complexes (abstract regular polytopes).
In elementary geometry, a polytope is a geometric object with flat sides (faces). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions n as an n-dimensional polytope or n-polytope. For example, a two-dimensional polygon is a 2-polytope and a three-dimensional polyhedron is a 3-polytope. In this context, "flat sides" means that the sides of a (k + 1)-polytope consist of k-polytopes that may have (k – 1)-polytopes in common.
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex.
In mathematics, the 11-cell is a self-dual abstract regular 4-polytope. Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. It has Schläfli type {3,5,3}, with 3 hemi-icosahedra around each edge.
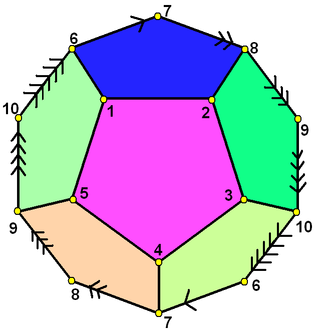
In mathematics, the 57-cell (pentacontaheptachoron) is a self-dual abstract regular 4-polytope. Its 57 cells are hemi-dodecahedra. It also has 57 vertices, 171 edges and 171 two-dimensional faces.
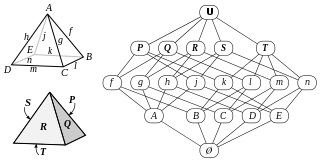
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines.
In spherical geometry, an n-gonalhosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.
171 is the natural number following 170 and preceding 172.
In geometry, an apeirogon or infinite polygon is a polygon with an infinite number of sides. Apeirogons are the rank 2 case of infinite polytopes. In some literature, the term "apeirogon" may refer only to the regular apeirogon, with an infinite dihedral group of symmetries.
In (polyhedral) geometry, a flag is a sequence of faces of a polytope, each contained in the next, with exactly one face from each dimension.
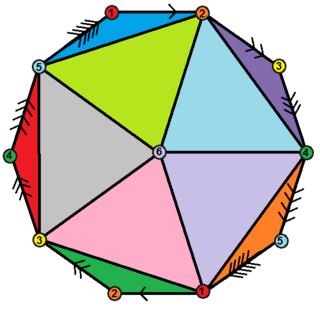
In geometry, a hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron, which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts.
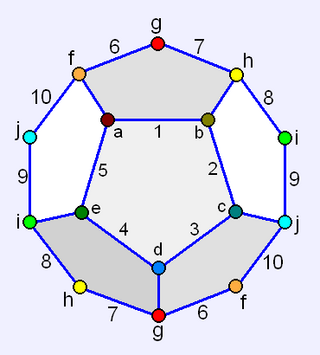
In geometry, a hemi-dodecahedron is an abstract, regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron, which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts.
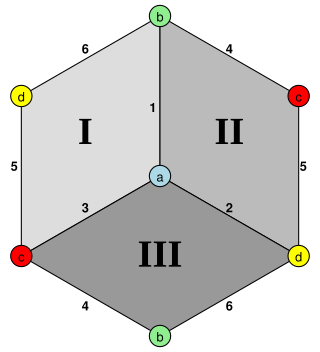
In abstract geometry, a hemicube is an abstract, regular polyhedron, containing half the faces of a cube.
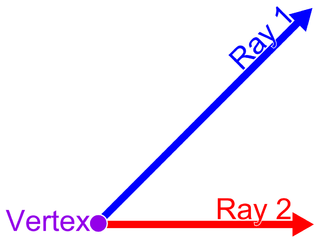
In geometry, a vertex is a point where two or more curves, lines, or edges meet or intersect. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices.
In geometry, an apeirotope or infinite polytope is a generalized polytope which has infinitely many facets.
In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon in which every n – 1 consecutive sides belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a regular polyhedron is a skew polygon such that every two consecutive sides belongs to one of the faces. Petrie polygons are named for mathematician John Flinders Petrie.
In mathematics, a regular 4-polytope or regular polychoron is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
In geometry, a hemi-octahedron is an abstract regular polyhedron, containing half the faces of a regular octahedron.
In the study of abstract polytopes, a chiral polytope is a polytope that is as symmetric as possible without being mirror-symmetric, formalized in terms of the action of the symmetry group of the polytope on its flags.
Peter McMullen is a British mathematician, a professor emeritus of mathematics at University College London.
In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron. They have either skew regular faces or skew regular vertex figures.
| International | |
|---|---|
| National | |
| Academics | |
| Other | |
   | This article about an American mathematician is a stub. You can help Wikipedia by expanding it. |
