
The Mach number, often only Mach, is a dimensionless quantity in fluid dynamics representing the ratio of flow velocity past a boundary to the local speed of sound. It is named after the Austrian physicist and philosopher Ernst Mach.

A pitot tube measures fluid flow velocity. It was invented by a French engineer, Henri Pitot, in the early 18th century, and was modified to its modern form in the mid-19th century by a French scientist, Henry Darcy. It is widely used to determine the airspeed of aircraft; the water speed of boats; and the flow velocity of liquids, air, and gases in industry.
In fluid mechanics, the Rayleigh number (Ra, after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 106 to 108.

Bernoulli's principle is a key concept in fluid dynamics that relates pressure, speed and height. Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or the fluid's potential energy. The principle is named after the Swiss mathematician and physicist Daniel Bernoulli, who published it in his book Hydrodynamica in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form.
In fluid dynamics, the Darcy–Weisbach equation is an empirical equation that relates the head loss, or pressure loss, due to friction along a given length of pipe to the average velocity of the fluid flow for an incompressible fluid. The equation is named after Henry Darcy and Julius Weisbach. Currently, there is no formula more accurate or universally applicable than the Darcy-Weisbach supplemented by the Moody diagram or Colebrook equation.
In fluid dynamics, the lift coefficient is a dimensionless quantity that relates the lift generated by a lifting body to the fluid density around the body, the fluid velocity and an associated reference area. A lifting body is a foil or a complete foil-bearing body such as a fixed-wing aircraft. CL is a function of the angle of the body to the flow, its Reynolds number and its Mach number. The section lift coefficient cl refers to the dynamic lift characteristics of a two-dimensional foil section, with the reference area replaced by the foil chord.
The Knudsen number (Kn) is a dimensionless number defined as the ratio of the molecular mean free path length to a representative physical length scale. This length scale could be, for example, the radius of a body in a fluid. The number is named after Danish physicist Martin Knudsen (1871–1949).

In aviation, airspeed is the speed of an aircraft relative to the air. Among the common conventions for qualifying airspeed are:
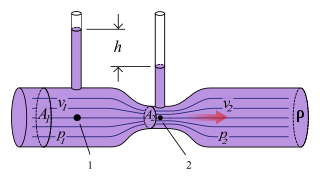
The Venturi effect is the reduction in fluid pressure that results when a fluid flows through a constricted section of a pipe. The Venturi effect is named after its discoverer, the 18th-century Italian physicist Giovanni Battista Venturi.

The true airspeed of an aircraft is the speed of the aircraft relative to the air mass through which it is flying. The true airspeed is important information for accurate navigation of an aircraft. Traditionally it is measured using an analogue TAS indicator, but as the Global Positioning System has become available for civilian use, the importance of such air-measuring instruments has decreased. Since indicated, as opposed to true, airspeed is a better indicator of margin above the stall, true airspeed is not used for controlling the aircraft; for these purposes the indicated airspeed – IAS or KIAS – is used. However, since indicated airspeed only shows true speed through the air at standard sea level pressure and temperature, a TAS meter is necessary for navigation purposes at cruising altitude in less dense air. The IAS meter reads very nearly the TAS at lower altitude and at lower speed. On jet airliners the TAS meter is usually hidden at speeds below 200 knots (370 km/h). Neither provides for accurate speed over the ground, since surface winds or winds aloft are not taken into account.
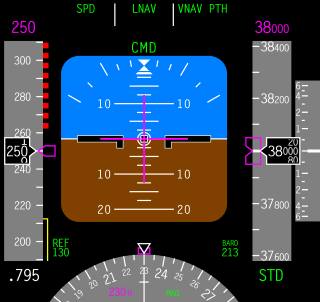
Indicated airspeed (IAS) is the airspeed of an aircraft as measured by its pitot-static system and displayed by the airspeed indicator (ASI). This is the pilots' primary airspeed reference.
The Einstein–Hilbert action in general relativity is the action that yields the Einstein field equations through the stationary-action principle. With the (− + + +) metric signature, the gravitational part of the action is given as
In aviation, calibrated airspeed (CAS) is indicated airspeed corrected for instrument and position error.
There are two different Bejan numbers (Be) used in the scientific domains of thermodynamics and fluid mechanics. Bejan numbers are named after Adrian Bejan.

The Stokes number (Stk), named after George Gabriel Stokes, is a dimensionless number characterising the behavior of particles suspended in a fluid flow. The Stokes number is defined as the ratio of the characteristic time of a particle to a characteristic time of the flow or of an obstacle, or
In fluid mechanics the term static pressure has several uses:

A Machmeter is an aircraft pitot-static system flight instrument that shows the ratio of the true airspeed to the speed of sound, a dimensionless quantity called Mach number. This is shown on a Machmeter as a decimal fraction. An aircraft flying at the speed of sound is flying at a Mach number of one, expressed as Mach 1.
In compressible fluid dynamics, impact pressure is the difference between total pressure and static pressure. In aerodynamics notation, this quantity is denoted as or .
In a nozzle or other constriction, the discharge coefficient is the ratio of the actual discharge to the ideal discharge, i.e., the ratio of the mass flow rate at the discharge end of the nozzle to that of an ideal nozzle which expands an identical working fluid from the same initial conditions to the same exit pressures.
Blade element momentum theory is a theory that combines both blade element theory and momentum theory. It is used to calculate the local forces on a propeller or wind-turbine blade. Blade element theory is combined with momentum theory to alleviate some of the difficulties in calculating the induced velocities at the rotor.















