
In mathematics, a filter or order filter is a special subset of a partially ordered set (poset), describing "large" or "eventual" elements. Filters appear in order and lattice theory, but also topology, whence they originate. The notion dual to a filter is an order ideal.

In mathematics, especially order theory, a partial order on a set is an arrangement such that, for certain pairs of elements, one precedes the other. The word partial is used to indicate that not every pair of elements needs to be comparable; that is, there may be pairs for which neither element precedes the other. Partial orders thus generalize total orders, in which every pair is comparable.
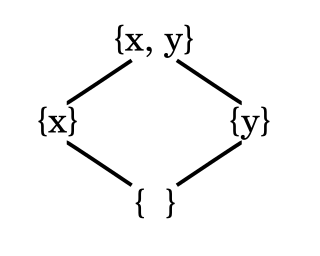
In order theory, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set one represents each element of as a vertex in the plane and draws a line segment or curve that goes upward from one vertex to another vertex whenever covers . These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary.
This is a glossary of some terms used in various branches of mathematics that are related to the fields of order, lattice, and domain theory. Note that there is a structured list of order topics available as well. Other helpful resources might be the following overview articles:
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum and a unique infimum. An example is given by the power set of a set, partially ordered by inclusion, for which the supremum is the union and the infimum is the intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor.
In mathematical order theory, an ideal is a special subset of a partially ordered set (poset). Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion. Ideals are of great importance for many constructions in order and lattice theory.
In mathematics, the phrase complete partial order is variously used to refer to at least three similar, but distinct, classes of partially ordered sets, characterized by particular completeness properties. Complete partial orders play a central role in theoretical computer science: in denotational semantics and domain theory.
In order theory, a branch of mathematics, an order embedding is a special kind of monotone function, which provides a way to include one partially ordered set into another. Like Galois connections, order embeddings constitute a notion which is strictly weaker than the concept of an order isomorphism. Both of these weakenings may be understood in terms of category theory.

In geometry and combinatorics, an arrangement of hyperplanes is an arrangement of a finite set A of hyperplanes in a linear, affine, or projective space S. Questions about a hyperplane arrangement A generally concern geometrical, topological, or other properties of the complement, M(A), which is the set that remains when the hyperplanes are removed from the whole space. One may ask how these properties are related to the arrangement and its intersection semilattice. The intersection semilattice of A, written L(A), is the set of all subspaces that are obtained by intersecting some of the hyperplanes; among these subspaces are S itself, all the individual hyperplanes, all intersections of pairs of hyperplanes, etc. (excluding, in the affine case, the empty set). These intersection subspaces of A are also called the flats ofA. The intersection semilattice L(A) is partially ordered by reverse inclusion.

In mathematics, in the branch of combinatorics, a graded poset is a partially-ordered set (poset) P equipped with a rank functionρ from P to the set N of all natural numbers. ρ must satisfy the following two properties:

In mathematics, Young's lattice is a lattice that is formed by all integer partitions. It is named after Alfred Young, who, in a series of papers On quantitative substitutional analysis, developed the representation theory of the symmetric group. In Young's theory, the objects now called Young diagrams and the partial order on them played a key, even decisive, role. Young's lattice prominently figures in algebraic combinatorics, forming the simplest example of a differential poset in the sense of Stanley (1988). It is also closely connected with the crystal bases for affine Lie algebras.
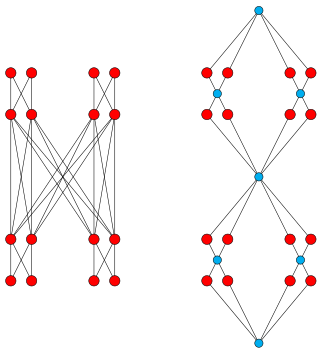
In mathematics, specifically order theory, the Dedekind–MacNeille completion of a partially ordered set is the smallest complete lattice that contains it. It is named after Holbrook Mann MacNeille whose 1937 paper first defined and constructed it, and after Richard Dedekind because its construction generalizes the Dedekind cuts used by Dedekind to construct the real numbers from the rational numbers. It is also called the completion by cuts or normal completion.
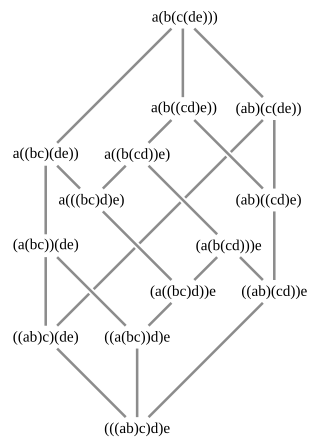
In mathematics, a Tamari lattice, introduced by Dov Tamari (1962), is a partially ordered set in which the elements consist of different ways of grouping a sequence of objects into pairs using parentheses; for instance, for a sequence of four objects abcd, the five possible groupings are ((ab)c)d, (ab)(cd), (a(bc))d, a((bc)d), and a(b(cd)). Each grouping describes a different order in which the objects may be combined by a binary operation; in the Tamari lattice, one grouping is ordered before another if the second grouping may be obtained from the first by only rightward applications of the associative law (xy)z = x(yz). For instance, applying this law with x = a, y = bc, and z = d gives the expansion (a(bc))d = a((bc)d), so in the ordering of the Tamari lattice (a(bc))d ≤ a((bc)d).
In the mathematical field of graph theory, the Fibonacci cubes or Fibonacci networks are a family of undirected graphs with rich recursive properties derived from its origin in number theory. Mathematically they are similar to the hypercube graphs, but with a Fibonacci number of vertices. Fibonacci cubes were first explicitly defined in Hsu (1993) in the context of interconnection topologies for connecting parallel or distributed systems. They have also been applied in chemical graph theory.
In mathematics, a differential poset is a partially ordered set satisfying certain local properties. This family of posets was introduced by Stanley (1988) as a generalization of Young's lattice, many of whose combinatorial properties are shared by all differential posets. In addition to Young's lattice, the other most significant example of a differential poset is the Young–Fibonacci lattice.
In mathematics, an incidence poset or incidence order is a type of partially ordered set that represents the incidence relation between vertices and edges of an undirected graph. The incidence poset of a graph G has an element for each vertex or edge in G; in this poset, there is an order relation x ≤ y if and only if either x = y or x is a vertex, y is an edge, and x is an endpoint of y.
Effect algebras are partial algebras which abstract the (partial) algebraic properties of events that can be observed in quantum mechanics. Structures equivalent to effect algebras were introduced by three different research groups in theoretical physics or mathematics in the late 1980s and early 1990s. Since then, their mathematical properties and physical as well as computational significance have been studied by researchers in theoretical physics, mathematics and computer science.
The order polynomial is a polynomial studied in mathematics, in particular in algebraic graph theory and algebraic combinatorics. The order polynomial counts the number of order-preserving maps from a poset to a chain of length . These order-preserving maps were first introduced by Richard P. Stanley while studying ordered structures and partitions as a Ph.D. student at Harvard University in 1971 under the guidance of Gian-Carlo Rota.
In order theory, a continuous poset is a partially ordered set in which every element is the directed supremum of elements approximating it.












