Fibonacci cube

Last updated August 24, 2024

In the mathematical field of graph theory, the Fibonacci cubes or Fibonacci networks are a family of undirected graphs with rich recursive properties derived from its origin in number theory. Mathematically they are similar to the hypercube graphs, but with a Fibonacci number of vertices. Fibonacci cubes were first explicitly defined in Hsu (1993) in the context of interconnection topologies for connecting parallel or distributed systems. They have also been applied in chemical graph theory.

Definition

Like the hypercube graph, the vertices of the Fibonacci cube of order n may be labeled with bitstrings of length n, in such a way that two vertices are adjacent whenever their labels differ in a single bit. However, in a Fibonacci cube, the only labels that are allowed are bitstrings with no two consecutive 1 bits. If the labels of the hypercube are interpreted as binary numbers, the labels in the Fibonacci cube are a subset, the fibbinary numbers. There are F_n + 2 labels possible, where F_n denotes the nth Fibonacci number, and therefore there are F_n + 2 vertices in the Fibonacci cube of order n.

Fibonacci cubes (drawn in red) as subgraphs of hypercubes FibboCube.png — Fibonacci cubes (drawn in red) as subgraphs of hypercubes

The nodes of such a network may be assigned consecutive integers from 0 to F_n + 2 − 1; the bitstrings corresponding to these numbers are given by their Zeckendorf representations.^[1]

Algebraic structure

The Fibonacci cube of order n is the simplex graph of the complement graph of an n-vertex path graph.^[2] That is, each vertex in the Fibonacci cube represents a clique in the path complement graph, or equivalently an independent set in the path itself; two Fibonacci cube vertices are adjacent if the cliques or independent sets that they represent differ by the addition or removal of a single element. Therefore, like other simplex graphs, Fibonacci cubes are median graphs and more generally partial cubes.^[3] The median of any three vertices in a Fibonacci cube may be found by computing the bitwise majority function of the three labels; if each of the three labels has no two consecutive 1 bits, the same is true of their majority.

The Fibonacci cube is also the graph of a distributive lattice that may be obtained via Birkhoff's representation theorem from a zigzag poset, a partially ordered set defined by an alternating sequence of order relations a<b>c<d>e<f> ...^[4] There is also an alternative graph-theoretic description of the same lattice: the independent sets of any bipartite graph may be given a partial order in which one independent set is less than another if they differ by removing elements from one side of the bipartition and adding elements to the other side of the bipartition; with this order, the independent sets form a distributive lattice,^[5] and applying this construction to a path graph results in the lattice associated with the Fibonacci cube.

Properties and algorithms

The Fibonacci cube of order n may be partitioned into a Fibonacci cube of order n − 1 (the nodes with labels beginning with a 0 bit) and a Fibonacci cube of order n − 2 (the nodes with labels beginning with a 1 bit).^[6]

Every Fibonacci cube has a Hamiltonian path. More specifically, there exists a path that obeys the partition described above: it visits the nodes with first bit 0 and the nodes with first bit 1 in two contiguous subsequences. Within these two subsequences, the path can be constructed recursively by the same rule, linking the two subsequences at the ends of the subsequences at which the second bit is 0. Thus, e.g., in the Fibonacci cube of order 4, the sequence constructed in this way is (0100-0101-0001-0000-0010)-(1010-1000-1001), where the parentheses demark the subsequences within the two subgraphs of the partition. Fibonacci cubes with an even number of nodes greater than two have a Hamiltonian cycle.^[7]

Munarini & Salvi (2002) investigate the radius and independence number of Fibonacci cubes. Because these graphs are bipartite and have Hamiltonian paths, their maximum independent sets have a number of vertices that is equal to half of the number of vertices in the whole graph, rounded up to the nearest integer.^[8] The diameter of a Fibonacci cube of order n is n, and its radius is n/2 (again, rounded up to the nearest integer).^[9]

Taranenko & Vesel (2007) showed that it is possible to test whether a graph is a Fibonacci cube in time near-linear in its size.

Applications

Hsu (1993) and Hsu, Page & Liu (1993) suggested using Fibonacci cubes as a network topology in parallel computing. As a communications network, the Fibonacci cube has beneficial properties similar to those of the hypercube: the number of incident edges per vertex is at most n/2 and the diameter of the network is at most n, both proportional to the logarithm of the number of vertices, and the ability of the network to be partitioned into smaller networks of the same type allows it to be split among multiple parallel computation tasks.^[7] Fibonacci cubes also support efficient protocols for routing and broadcasting in distributed computations.^[10]

Klavžar & Žigert (2005) apply Fibonacci cubes in chemical graph theory as a description of the family of perfect matchings of certain molecular graphs. For a molecular structure described by a planar graph G, the resonance graph or (Z-transformation graph) of G is a graph whose vertices describe perfect matchings of G and whose edges connect pairs of perfect matchings whose symmetric difference is an interior face of G. Polycyclic aromatic hydrocarbons may be described as subgraphs of a hexagonal tiling of the plane, and the resonance graph describes possible double-bond structures of these molecules. As Klavžar & Žigert (2005) show, hydrocarbons formed by chains of hexagons, linked edge-to-edge with no three adjacent hexagons in a line, have resonance graphs that are exactly the Fibonacci graphs. More generally Zhang, Ou & Yao (2009) described the class of planar bipartite graphs that have Fibonacci cubes as their resonance graphs.^[2]

Related graphs

Generalized Fibonacci cubes were presented by Hsu & Chung (1993) based on the k-th order Fibonacci numbers, which were later further extended to a larger class of networks called the Linear Recursive Networks by Hsu, Chung & Das (1997) based on more general forms of linear recursions. Wu (1997) modified the second order Fibonacci cubes based on different initial conditions. Another related graph is the Lucas cube, a graph with a Lucas number of vertices defined from the Fibonacci cube by forbidding a 1 bit in both the first and last positions of each bitstring; Dedó, Torri & Salvi (2002) investigated the coloring properties of both Fibonacci cubes and Lucas cubes.

Notes

↑ Klavžar (2011), pp. 3–4.
1 2 Klavžar (2011), p.3.
↑ Klavžar (2005); Klavžar (2011), Theorem 5.1, p.10.
↑ Gansner (1982) calls the fact that this lattice has a Fibonacci number of elements a “well known fact,” while Stanley (1986) asks for a description of it in an exercise. See also Höft & Höft (1985), Beck (1990), and Salvi & Salvi (2008).
↑ Propp (1997).
↑ Klavžar (2011), pp. 4–5.
1 2 Cong, Zheng & Sharma (1993).
↑ Klavžar (2011), p.6.
↑ Klavžar (2011), p.9.
↑ Hsu (1993); Stojmenovic 1998.

Related Research Articles

<span class="mw-page-title-main">Hypercube</span> Convex polytope, the n-dimensional analogue of a square and a cube

In geometry, a hypercube is an n-dimensional analogue of a square and a cube. It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to $.$

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets $and, that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.$

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most $k$ different colors, for a given value of $k$ , or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In mathematics, a universal graph is an infinite graph that contains every finite graph as an induced subgraph. A universal graph of this type was first constructed by Richard Rado and is now called the Rado graph or random graph. More recent work has focused on universal graphs for a graph family $F$ : that is, an infinite graph belonging to F that contains all finite graphs in $F$ . For instance, the Henson graphs are universal in this sense for the $i$ -clique-free graphs.

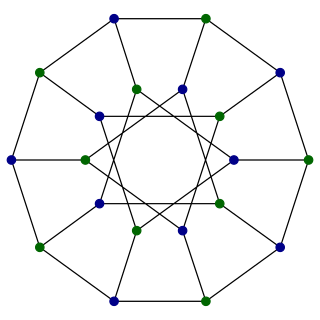
<span class="mw-page-title-main">Desargues graph</span> Distance-transitive cubic graph with 20 nodes and 30 edges

In the mathematical field of graph theory, the Desargues graph is a distance-transitive, cubic graph with 20 vertices and 30 edges. It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.

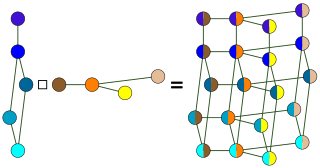
<span class="mw-page-title-main">Cartesian product of graphs</span> Operation in graph theory

In graph theory, the Cartesian product $G □ H$ of graphs $G$ and $H$ is a graph such that:

<span class="mw-page-title-main">Hypercube graph</span> Graphs formed by a hypercubes edges and vertices

In graph theory, the hypercube graph $Q n$ is the graph formed from the vertices and edges of an $n$ -dimensional hypercube. For instance, the cube graph $Q 3$ is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. $Q n$ has $2 n$ vertices, $2 n - 1 n$ edges, and is a regular graph with $n$ edges touching each vertex.

In graph theory, the cube-connected cycles is an undirected cubic graph, formed by replacing each vertex of a hypercube graph by a cycle. It was introduced by Preparata & Vuillemin (1981) for use as a network topology in parallel computing.

In graph theory, a division of mathematics, a median graph is an undirected graph in which every three vertices a, b, and c have a unique median: a vertex m(a,b,c) that belongs to shortest paths between each pair of a, b, and c.

In graph theory, a branch of mathematics, the simplex graph $κ(G)$ of an undirected graph $G$ is itself a graph, with one node for each clique (a set of mutually adjacent vertices) in $G$ . Two nodes of $κ(G)$ are linked by an edge whenever the corresponding two cliques differ in the presence or absence of a single vertex.

In mathematics, a fence, also called a zigzag poset, is a partially ordered set (poset) in which the order relations form a path with alternating orientations:

<span class="mw-page-title-main">Young–Fibonacci lattice</span>

In mathematics, the Young–Fibonacci graph and Young–Fibonacci lattice, named after Alfred Young and Leonardo Fibonacci, are two closely related structures involving sequences of the digits 1 and 2. Any digit sequence of this type can be assigned a rank, the sum of its digits: for instance, the rank of 11212 is 1 + 1 + 2 + 1 + 2 = 7. As was already known in ancient India, the number of sequences with a given rank is a Fibonacci number. The Young–Fibonacci lattice is an infinite modular lattice having these digit sequences as its elements, compatible with this rank structure. The Young–Fibonacci graph is the graph of this lattice, and has a vertex for each digit sequence. As the graph of a modular lattice, it is a modular graph.

In graph theory, a folded cube graph is an undirected graph formed from a hypercube graph by adding to it a perfect matching that connects opposite pairs of hypercube vertices.

In graph theory, a partial cube is a graph that is an isometric subgraph of a hypercube. In other words, a partial cube can be identified with a subgraph of a hypercube in such a way that the distance between any two vertices in the partial cube is the same as the distance between those vertices in the hypercube. Equivalently, a partial cube is a graph whose vertices can be labeled with bit strings of equal length in such a way that the distance between two vertices in the graph is equal to the Hamming distance between their labels. Such a labeling is called a Hamming labeling; it represents an isometric embedding of the partial cube into a hypercube.

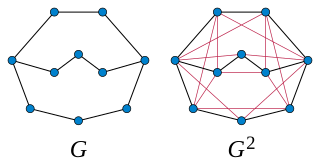
In graph theory, a branch of mathematics, the $k$ th power $G k$ of an undirected graph $G$ is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in $G$ is at most $k$ . Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: $G 2$ is called the square of $G$ , $G 3$ is called the cube of $G$ , etc.

<span class="mw-page-title-main">Halved cube graph</span> Graph of the vertices and edges of a demihypercube

In graph theory, the halved cube graph or half cube graph of dimension $n$ is the graph of the demihypercube, formed by connecting pairs of vertices at distance exactly two from each other in the hypercube graph. That is, it is the half-square of the hypercube. This connectivity pattern produces two isomorphic graphs, disconnected from each other, each of which is the halved cube graph.

<span class="mw-page-title-main">Hypercube internetwork topology</span> Type of network topology

In computer networking, hypercube networks are a type of network topology used to connect and route data between multiple processing units or computers. Hypercube networks consist of $2 m$ nodes, which form the vertices of squares to create an internetwork connection. A hypercube is basically a multidimensional mesh network with two nodes in each dimension. Due to similarity, such topologies are usually grouped into a $k$ -ary $d$ -dimensional mesh topology family, where $d$ represents the number of dimensions and $k$ represents the number of nodes in each dimension.

In graph theory, the shuffle-exchange network is an undirected cubic multigraph, whose vertices represent binary sequences of a given length and whose edges represent two operations on these sequence, circular shifts and flipping the lowest-order bit.

References

Beck, István (1990), "Partial orders and the Fibonacci numbers", Fibonacci Quarterly , 28 (2): 172–174, MR 1051291 .
Cong, B.; Zheng, S. Q.; Sharma, S. (1993), "On simulations of linear arrays, rings and 2D meshes on Fibonacci cube networks", Proc. 7th Int. Parallel Processing Symposium , pp. 748–751, doi:10.1109/IPPS.1993.262788, ISBN 0-8186-3442-1, S2CID 621063 .
Dedó, Ernesto; Torri, Damiano; Salvi, Norma Zagaglia (2002), "The observability of the Fibonacci and the Lucas cubes", Discrete Mathematics , 255 (1–3): 55–63, doi: 10.1016/S0012-365X(01)00387-9 .
Gansner, Emden R. (1982), "On the lattice of order ideals of an up-down poset", Discrete Mathematics, 39 (2): 113–122, doi: 10.1016/0012-365X(82)90134-0 , MR 0675856 .
Höft, Hartmut; Höft, Margret (1985), "A Fibonacci sequence of distributive lattices", Fibonacci Quarterly , 23 (3): 232–237, MR 0806293 .
Hsu, W.-J. (1993), "Fibonacci cubes: a new interconnection topology", IEEE Transactions on Parallel and Distributed Systems, 4 (1): 3–12, doi:10.1109/71.205649 .
Hsu, W.-J.; Chung, M. J. (1993), "Generalized Fibonacci cubes", 1993 International Conference on Parallel Processing - ICPP'93, vol. 1, pp. 299–302, doi:10.1109/ICPP.1993.95, ISBN 0-8493-8983-6, S2CID 15982621 .
Hsu, W.-J.; Page, C. V.; Liu, J.-S. (1993), "Fibonacci cubes: a class of self-similar graphs", Fibonacci Quarterly , 31 (1): 65–72.
Hsu, W.-J.; Chung, M. J.; Das, A. (1997), "Linear recursive networks and their applications in distributed systems", IEEE Transactions on Parallel and Distributed Systems , 8 (7): 673–680, doi:10.1109/71.598343 .
Klavžar, Sandi (2005), "On median nature and enumerative properties of Fibonacci-like cubes", Discrete Mathematics, 299 (1–3): 145–153, doi: 10.1016/j.disc.2004.02.023 .
Klavžar, Sandi (2011), "Structure of Fibonacci cubes: a survey" (PDF), IMFM Preprint Series, 49 (1150), Ljubljana, Slovenia: Institute of Mathematics, Physics and Mechanics.
Klavžar, Sandi; Žigert, Petra (2005), "Fibonacci cubes are the resonance graphs of Fibonaccenes", Fibonacci Quarterly , 43 (3): 269–276, archived from the original on 2007-02-08.
Munarini, Emanuele; Salvi, Norma Zagaglia (2002), "Structural and enumerative properties of the Fibonacci cubes", Discrete Mathematics, 255 (1–3): 317–324, doi: 10.1016/S0012-365X(01)00407-1 .
Propp, James (1997), "Generating random elements of finite distributive lattices", Electronic Journal of Combinatorics, 4 (2): R15, arXiv: math.CO/9801066 , doi:10.37236/1330, S2CID 13313188 .
Salvi, Rodolfo; Salvi, Norma Zagaglia (2008), "Alternating unimodal sequences of Whitney numbers", Ars Combinatoria , 87: 105–117, MR 2414008 .
Stanley, Richard P. (1986), Enumerative Combinatorics, Wadsworth, Inc. Exercise 3.23a, page 157.
Stojmenovic, Ivan (1998), "Optimal deadlock-free routing and broadcasting on Fibonacci cube networks" (PDF), Utilitas Mathematica, 53: 159–166, archived from the original (PDF) on 2011-07-25.
Taranenko, A.; Vesel, A. (2007), "Fast recognition of Fibonacci cubes", Algorithmica, 49 (2): 81–93, doi:10.1007/s00453-007-9026-5, S2CID 993779 .
Wu, Jie (1997), "Extended Fibonacci cubes", IEEE Transactions on Parallel and Distributed Systems, 8 (12): 1203–1210, doi:10.1109/71.640012 .
Zhang, Heping; Ou, Lifeng; Yao, Haiyuan (2009), "Fibonacci-like cubes as Z-transformation graphs", Discrete Mathematics, 309 (6): 1284–1293, doi: 10.1016/j.disc.2008.01.053 , MR 2510538 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Klavžar (2011), pp. 3–4.

[k11-3-2] 1 2 Klavžar (2011), p.3.

[3] Klavžar (2005); Klavžar (2011), Theorem 5.1, p.10.

[4] Gansner (1982) calls the fact that this lattice has a Fibonacci number of elements a “well known fact,” while Stanley (1986) asks for a description of it in an exercise. See also Höft & Höft (1985), Beck (1990), and Salvi & Salvi (2008).

[5] Propp (1997).

[6] Klavžar (2011), pp. 4–5.

[CZS-7] 1 2 Cong, Zheng & Sharma (1993).

[8] Klavžar (2011), p.6.

[9] Klavžar (2011), p.9.

[10] Hsu (1993); Stojmenovic 1998.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]