Simplex graph

Last updated June 21, 2023 • 3 min readFrom Wikipedia, The Free Encyclopedia

In graph theory, a branch of mathematics, the simplex graph $κ(G)$ of an undirected graph $G$ is itself a graph, with one node for each clique (a set of mutually adjacent vertices) in $G$ . Two nodes of $κ(G)$ are linked by an edge whenever the corresponding two cliques differ in the presence or absence of a single vertex.

The empty set is included as one of the cliques of $G$ that are used to form the clique graph, as is every set of one vertex and every set of two adjacent vertices. Therefore, the simplex graph contains within it a subdivision of $G$ itself. The simplex graph of a complete graph is a hypercube graph, and the simplex graph of a cycle graph of length four or more is a gear graph. The simplex graph of the complement graph of a path graph is a Fibonacci cube.

The complete subgraphs of $G$ can be given the structure of a median algebra: the median of three cliques $A$ , $B$ , and $C$ is formed by the vertices that belong to a majority of the three cliques.^[1] Any two vertices belonging to this median set must both belong to at least one of $A$ , $B$ , or $C$ , and therefore must be linked by an edge, so the median of three cliques is itself a clique. The simplex graph is the median graph corresponding to this median algebra structure. When $G$ is the complement graph of a bipartite graph, the cliques of $G$ can be given a stronger structure as a distributive lattice,^[2] and in this case the simplex graph is the graph of the lattice. As is true for median graphs more generally, every simplex graph is itself bipartite.

The simplex graph has one vertex for every simplex in the clique complex $X (G)$ of $G$ , and two vertices are linked by an edge when one of the two corresponding simplexes is a facet of the other. Thus, the objects (vertices in the simplex graph, simplexes in $X (G)$ ) and relations between objects (edges in the simplex graph, inclusion relations between simplexes in $X (G)$ ) are in one-to-one correspondence between $X (G)$ and $κ(G)$ .

Simplex graphs were introduced by Bandelt & van de Vel (1989),^[3] who observed that a simplex graph has no cubes if and only if the underlying graph is triangle-free, and showed that the chromatic number of the underlying graph equals the minimum number $n$ such that the simplex graph can be isometrically embedded into a Cartesian product of $n$ trees. As a consequence of the existence of triangle-free graphs with high chromatic number, they showed that there exist two-dimensional topological median algebras that cannot be embedded into products of finitely many real trees. Imrich, Klavžar & Mulder (1999) also use simplex graphs as part of their proof that testing whether a graph is triangle-free or whether it is a median graph may be performed equally quickly.

Notes

↑ Barthélemy, Leclerc & Monjardet (1986), page 200.
↑ Propp (1997).
↑ Imrich, Klavžar & Mulder (1999) credit the introduction of simplex graphs to a later paper, also by Bandelt and van de Vel, but this appears to be a mistake.

Related Research Articles

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets $and, that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.$

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In the mathematical area of graph theory, a clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. That is, a clique of a graph $is an induced subgraph of that is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. Cliques have also been studied in computer science: the task of finding whether there is a clique of a given size in a graph is NP-complete, but despite this hardness result, many algorithms for finding cliques have been studied.$

In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.

<span class="mw-page-title-main">Perfect graph</span> Graph with tight clique-coloring relation

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

In the mathematical discipline of graph theory, the line graph of an undirected graph $G$ is another graph $L(G)$ that represents the adjacencies between edges of $G$ . $L(G)$ is constructed in the following way: for each edge in $G$ , make a vertex in $L(G)$ ; for every two edges in $G$ that have a vertex in common, make an edge between their corresponding vertices in $L(G)$ .

<span class="mw-page-title-main">Desargues graph</span> Distance-transitive cubic graph with 20 nodes and 30 edges

In the mathematical field of graph theory, the Desargues graph is a distance-transitive, cubic graph with 20 vertices and 30 edges. It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.

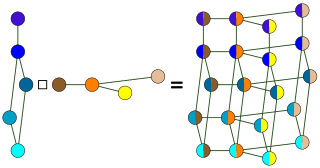
<span class="mw-page-title-main">Cartesian product of graphs</span> Operation in graph theory

In graph theory, the Cartesian product $G □ H$ of graphs $G$ and $H$ is a graph such that:

<span class="mw-page-title-main">Tensor product of graphs</span> Operation in graph theory

In graph theory, the tensor product $G \times H$ of graphs $G$ and $H$ is a graph such that

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.

In graph theory, a division of mathematics, a median graph is an undirected graph in which every three vertices a, b, and c have a unique median: a vertex m(a,b,c) that belongs to shortest paths between each pair of a, b, and c.

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

<span class="mw-page-title-main">Squaregraph</span> Planar graph with quadrilateral faces

In graph theory, a branch of mathematics, a squaregraph is a type of undirected graph that can be drawn in the plane in such a way that every bounded face is a quadrilateral and every vertex with three or fewer neighbors is incident to an unbounded face.

Clique complexes, independence complexes, flag complexes, Whitney complexes and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques of an undirected graph.

In the mathematical field of graph theory, the Fibonacci cubes or Fibonacci networks are a family of undirected graphs with rich recursive properties derived from its origin in number theory. Mathematically they are similar to the hypercube graphs, but with a Fibonacci number of vertices. Fibonacci cubes were first explicitly defined in Hsu (1993) in the context of interconnection topologies for connecting parallel or distributed systems. They have also been applied in chemical graph theory.

In geometry and polyhedral combinatorics, an integral polytope is a convex polytope whose vertices all have integer Cartesian coordinates. That is, it is a polytope that equals the convex hull of its integer points. Integral polytopes are also called lattice polytopes or Z-polytopes. The special cases of two- and three-dimensional integral polytopes may be called polygons or polyhedra instead of polytopes, respectively.

In graph theory, a branch of combinatorial mathematics, a block graph or clique tree is a type of undirected graph in which every biconnected component (block) is a clique.

In graph theory, a partial cube is a graph that is isometric to a subgraph of a hypercube. In other words, a partial cube can be identified with a subgraph of a hypercube in such a way that the distance between any two vertices in the partial cube is the same as the distance between those vertices in the hypercube. Equivalently, a partial cube is a graph whose vertices can be labeled with bit strings of equal length in such a way that the distance between two vertices in the graph is equal to the Hamming distance between their labels. Such a labeling is called a Hamming labeling; it represents an isometric embedding of the partial cube into a hypercube.

<span class="mw-page-title-main">Convex subgraph</span>

In metric graph theory, a convex subgraph of an undirected graph G is a subgraph that includes every shortest path in G between two of its vertices. Thus, it is analogous to the definition of a convex set in geometry, a set that contains the line segment between every pair of its points.

In graph theory, a branch of mathematics, the modular graphs are undirected graphs in which every three vertices $x$ , $y$ , and $z$ have at least one median vertex $m (x, y, z)$ that belongs to shortest paths between each pair of $x$ , $y$ , and $z$ . Their name comes from the fact that a finite lattice is a modular lattice if and only if its Hasse diagram is a modular graph.

References

Bandelt, H.-J.; Chepoi, V. (2008), "Metric graph theory and geometry: a survey", in Goodman, J.E.; Pach, J.; Pollack, R. (eds.), Surveys on Discrete and Computational Geometry: Twenty Years Later, Contemp. Math., vol. 453, Providence, RI: AMS, pp. 49–86.
Bandelt, H.-J.; van de Vel, M. (1989), "Embedding topological median algebras in products of dendrons", Proceedings of the London Mathematical Society, s3-58 (3): 439–453, doi:10.1112/plms/s3-58.3.439, archived from the original on 2013-04-15.
Barthélemy, J.-P.; Leclerc, B.; Monjardet, B. (1986), "On the use of ordered sets in problems of comparison and consensus of classifications", Journal of Classification, 3 (2): 187–224, doi:10.1007/BF01894188, S2CID 6092438 .
Imrich, Wilfried; Klavžar, Sandi; Mulder, Henry Martyn (1999), "Median graphs and triangle-free graphs", SIAM Journal on Discrete Mathematics , 12 (1): 111–118, CiteSeerX 10.1.1.28.5906 , doi:10.1137/S0895480197323494, MR 1666073 .
Propp, James (1997), "Generating random elements of finite distributive lattices", Electronic Journal of Combinatorics, 4 (2): R15, arXiv: math.CO/9801066 , doi:10.37236/1330, S2CID 13313188 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Barthélemy, Leclerc & Monjardet (1986), page 200.

[2] Propp (1997).

[3] Imrich, Klavžar & Mulder (1999) credit the introduction of simplex graphs to a later paper, also by Bandelt and van de Vel, but this appears to be a mistake.

[1]

[2]

[3]