Clique complexes, independence complexes, flag complexes, Whitney complexes and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques (complete subgraphs) of an undirected graph.
The clique complexX(G) of an undirected graph G is an abstract simplicial complex (that is, a family of finite sets closed under the operation of taking subsets), formed by the sets of vertices in the cliques of G. Any subset of a clique is itself a clique, so this family of sets meets the requirement of an abstract simplicial complex that every subset of a set in the family should also be in the family.
The clique complex can also be viewed as a topological space in which each clique of k vertices is represented by a simplex of dimension k – 1. The 1-skeleton of X(G) (also known as the underlying graph of the complex) is an undirected graph with a vertex for every 1-element set in the family and an edge for every 2-element set in the family; it is isomorphic to G. [1]
Every clique complex is an abstract simplicial complex, but the opposite is not true. For example, consider the abstract simplicial complex over {1,2,3,4} with maximal sets {1,2,3},{2,3,4},{4,1}. If it were the X(G) of some graph G, then G had to have the edges {1,2},{1,3},{2,3},{2,4},{3,4},{4,1}, so X(G) should also contain the clique {1,2,3,4}.
The independence complex I(G) of an undirected graph G is an abstract simplicial complex formed by the sets of vertices in the independent sets of G. The clique complex of G is equivalent to the independence complex of the complement graph of G.
A flag complex is an abstract simplicial complex with an additional property called "2-determined": for every subset S of vertices, if every pair of vertices in S is in the complex, then S itself is in the complex too.
Every clique complex is a flag complex: if every pair of vertices in S is a clique of size 2, then there is an edge between them, so S is a clique.
Every flag complex is a clique complex: given a flag complex, define a graph G on the set of all vertices, where two vertices u,v are adjacent in G iff {u,v} is in the complex (this graph is called the 1-skeleton of the complex). By definition of a flag complex, every set of vertices that are pairwise-connected, is in the complex. Therefore, the flag complex is equal to the clique complex on G.
Thus, flag complexes and clique complexes are essentially the same thing. However, in many cases it is convenient to define a flag complex directly from some data other than a graph, rather than indirectly as the clique complex of a graph derived from that data. [2]
Mikhail Gromov defined the no-Δ condition to be the condition of being a flag complex.
Clique complexes are also known as Whitney complexes, after Hassler Whitney. A Whitney triangulation or clean triangulation of a two-dimensional manifold is an embedding of a graph G onto the manifold in such a way that every face is a triangle and every triangle is a face. If a graph G has a Whitney triangulation, it must form a cell complex that is isomorphic to the Whitney complex of G. In this case, the complex (viewed as a topological space) is homeomorphic to the underlying manifold. A graph G has a 2-manifold clique complex, and can be embedded as a Whitney triangulation, if and only if G is locally cyclic; this means that, for every vertex v in the graph, the induced subgraph formed by the neighbors of v forms a single cycle. [3]
The primal graph G(H) of a hypergraph is the graph on the same vertex set that has as its edges the pairs of vertices appearing together in the same hyperedge. A hypergraph is said to be conformal if every maximal clique of its primal graph is a hyperedge, or equivalently, if every clique of its primal graph is contained in some hyperedge. [4] If the hypergraph is required to be downward-closed (so it contains all hyperedges that are contained in some hyperedge) then the hypergraph is conformal precisely when it is a flag complex. This relates the language of hypergraphs to the language of simplicial complexes.
The barycentric subdivision of any cell complex C is a flag complex having one vertex per cell of C. A collection of vertices of the barycentric subdivision form a simplex if and only if the corresponding collection of cells of C form a flag (a chain in the inclusion ordering of the cells). [2] In particular, the barycentric subdivision of a cell complex on a 2-manifold gives rise to a Whitney triangulation of the manifold.
The order complex of a partially ordered set consists of the chains (totally ordered subsets) of the partial order. If every pair of some subset is itself ordered, then the whole subset is a chain, so the order complex satisfies the no-Δ condition. It may be interpreted as the clique complex of the comparability graph of the partial order. [2]
The matching complex of a graph consists of the sets of edges no two of which share an endpoint; again, this family of sets satisfies the no-Δ condition. It may be viewed as the clique complex of the complement graph of the line graph of the given graph. When the matching complex is referred to without any particular graph as context, it means the matching complex of a complete graph. The matching complex of a complete bipartite graph Km,n is known as a chessboard complex. It is the clique graph of the complement graph of a rook's graph, [5] and each of its simplices represents a placement of rooks on an m × n chess board such that no two of the rooks attack each other. When m = n ± 1, the chessboard complex forms a pseudo-manifold.
The Vietoris–Rips complex of a set of points in a metric space is a special case of a clique complex, formed from the unit disk graph of the points; however, every clique complex X(G) may be interpreted as the Vietoris–Rips complex of the shortest path metric on the underlying graph G.
Hodkinson & Otto (2003) describe an application of conformal hypergraphs in the logics of relational structures. In that context, the Gaifman graph of a relational structure is the same as the underlying graph of the hypergraph representing the structure, and a structure is guarded if it corresponds to a conformal hypergraph.
Gromov showed that a cubical complex (that is, a family of hypercubes intersecting face-to-face) forms a CAT(0) space if and only if the complex is simply connected and the link of every vertex forms a flag complex. A cubical complex meeting these conditions is sometimes called a cubing or a space with walls. [1] [6]
Meshulam [7] proves the following theorem on the homology of the clique complex. Given integers , suppose a graph G satisfies a property called , which means that:
Then the j-th reduced homology of the clique complex X(G) is trivial for any j between 0 and .
In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices.
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).
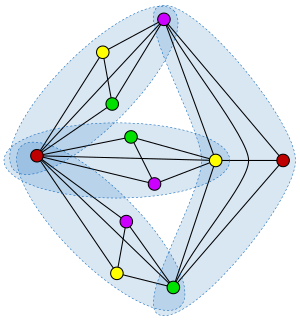
In graph theory, the Erdős–Faber–Lovász conjecture is a problem about graph coloring, named after Paul Erdős, Vance Faber, and László Lovász, who formulated it in 1972. It says:
In combinatorics, an abstract simplicial complex (ASC), often called an abstract complex or just a complex, is a family of sets that is closed under taking subsets, i.e., every subset of a set in the family is also in the family. It is a purely combinatorial description of the geometric notion of a simplicial complex. For example, in a 2-dimensional simplicial complex, the sets in the family are the triangles, their edges, and their vertices.
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:
In graph theory, a branch of mathematics, the circuit rank, cyclomatic number, cycle rank, or nullity of an undirected graph is the minimum number of edges that must be removed from the graph to break all its cycles, making it into a tree or forest. It is equal to the number of independent cycles in the graph. Unlike the corresponding feedback arc set problem for directed graphs, the circuit rank r is easily computed using the formula
In mathematics, topological graph theory is a branch of graph theory. It studies the embedding of graphs in surfaces, spatial embeddings of graphs, and graphs as topological spaces. It also studies immersions of graphs.
In the mathematical discipline of graph theory, the dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.
In graph theory, particularly in the theory of hypergraphs, the line graph of a hypergraphH, denoted L(H), is the graph whose vertex set is the set of the hyperedges of H, with two vertices adjacent in L(H) when their corresponding hyperedges have a nonempty intersection in H. In other words, L(H) is the intersection graph of a family of finite sets. It is a generalization of the line graph of a graph.
In graph theory, a well-covered graph is an undirected graph in which every minimal vertex cover has the same size as every other minimal vertex cover. Equivalently, these are the graphs in which all maximal independent sets have equal size. Well-covered graphs were defined and first studied by Michael D. Plummer in 1970.
In graph theory, a matching in a hypergraph is a set of hyperedges, in which every two hyperedges are disjoint. It is an extension of the notion of matching in a graph.
In graph theory, a vertex cover in a hypergraph is a set of vertices, such that every hyperedge of the hypergraph contains at least one vertex of that set. It is an extension of the notion of vertex cover in a graph.
In graph theory, the term bipartite hypergraph describes several related classes of hypergraphs, all of which are natural generalizations of a bipartite graph.
In the mathematical field of graph theory, Hall-type theorems for hypergraphs are several generalizations of Hall's marriage theorem from graphs to hypergraphs. Such theorems were proved by Ofra Kessler, Ron Aharoni, Penny Haxell, Roy Meshulam, and others.
In graph theory, a balanced hypergraph is a hypergraph that has several properties analogous to that of a bipartite graph.
The independence complex of a graph is a mathematical object describing the independent sets of the graph. Formally, the independence complex of an undirected graph G, denoted by I(G), is an abstract simplicial complex, formed by the sets of vertices in the independent sets of G. Any subset of an independent set is itself an independent set, so I(G) is indeed closed under taking subsets.
In graph theory, a rainbow-independent set (ISR) is an independent set in a graph, in which each vertex has a different color.
In graph theory, there are two related properties of a hypergraph that are called its "width". Given a hypergraph H =, we say that a set K of edges pins another set F of edges if every edge in F intersects some edge in K. Then:
