
Noether's theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law. This is the first of two theorems published by mathematician Emmy Noether in 1918. The action of a physical system is the integral over time of a Lagrangian function, from which the system's behavior can be determined by the principle of least action. This theorem only applies to continuous and smooth symmetries of physical space.

In physics, Hooke's law is an empirical law which states that the force needed to extend or compress a spring by some distance scales linearly with respect to that distance—that is, Fs = kx, where k is a constant factor characteristic of the spring, and x is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ut tensio, sic vis. Hooke states in the 1678 work that he was aware of the law since 1660.

In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time evolution of a Hamiltonian dynamical system. The Poisson bracket also distinguishes a certain class of coordinate transformations, called canonical transformations, which map canonical coordinate systems into canonical coordinate systems. A "canonical coordinate system" consists of canonical position and momentum variables that satisfy canonical Poisson bracket relations. The set of possible canonical transformations is always very rich. For instance, it is often possible to choose the Hamiltonian itself as one of the new canonical momentum coordinates.
Linear elasticity is a mathematical model as to how solid objects deform and become internally stressed by prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.

The path integral formulation is a description in quantum mechanics that generalizes the stationary action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.

In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. Propagators may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called (causal) Green's functions.
In mechanics, virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. The work of a force acting on a particle as it moves along a displacement is different for different displacements. Among all the possible displacements that a particle may follow, called virtual displacements, one will minimize the action. This displacement is therefore the displacement followed by the particle according to the principle of least action.
The work of a force on a particle along a virtual displacement is known as the virtual work.

In geometry and linear algebra, a Cartesian tensor uses an orthonormal basis to represent a tensor in a Euclidean space in the form of components. Converting a tensor's components from one such basis to another is done through an orthogonal transformation.
In mathematics, in particular in algebraic geometry and differential geometry, Dolbeault cohomology (named after Pierre Dolbeault) is an analog of de Rham cohomology for complex manifolds. Let M be a complex manifold. Then the Dolbeault cohomology groups depend on a pair of integers p and q and are realized as a subquotient of the space of complex differential forms of degree (p,q).
Elastic energy is the mechanical potential energy stored in the configuration of a material or physical system as it is subjected to elastic deformation by work performed upon it. Elastic energy occurs when objects are impermanently compressed, stretched or generally deformed in any manner. Elasticity theory primarily develops formalisms for the mechanics of solid bodies and materials. The elastic potential energy equation is used in calculations of positions of mechanical equilibrium. The energy is potential as it will be converted into other forms of energy, such as kinetic energy and sound energy, when the object is allowed to return to its original shape (reformation) by its elasticity.
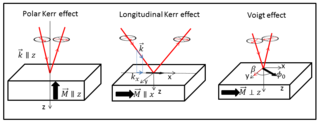
The Voigt effect is a magneto-optical phenomenon which rotates and elliptizes linearly polarised light sent into an optically active medium. The effect is named after the German scientist Woldemar Voigt who discovered it in vapors. Unlike many other magneto-optical effects such as the Kerr or Faraday effect which are linearly proportional to the magnetization, the Voigt effect is proportional to the square of the magnetization and can be seen experimentally at normal incidence. There are also other denominations for this effect, used interchangeably in the modern scientific literature: the Cotton–Mouton effect and magnetic-linear birefringence, with the latter reflecting the physical meaning of the effect.
The Frank–Tamm formula yields the amount of Cherenkov radiation emitted on a given frequency as a charged particle moves through a medium at superluminal velocity. It is named for Russian physicists Ilya Frank and Igor Tamm who developed the theory of the Cherenkov effect in 1937, for which they were awarded a Nobel Prize in Physics in 1958.
Lagrange brackets are certain expressions closely related to Poisson brackets that were introduced by Joseph Louis Lagrange in 1808–1810 for the purposes of mathematical formulation of classical mechanics, but unlike the Poisson brackets, have fallen out of use.
In continuum mechanics, a compatible deformation tensor field in a body is that unique tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.
Ashtekar variables, which were a new canonical formalism of general relativity, raised new hopes for the canonical quantization of general relativity and eventually led to loop quantum gravity. Smolin and others independently discovered that there exists in fact a Lagrangian formulation of the theory by considering the self-dual formulation of the Tetradic Palatini action principle of general relativity. These proofs were given in terms of spinors. A purely tensorial proof of the new variables in terms of triads was given by Goldberg and in terms of tetrads by Henneaux et al.

In geotechnical engineering, rock mass plasticity is the study of the response of rocks to loads beyond the elastic limit. Historically, conventional wisdom has it that rock is brittle and fails by fracture, while plasticity is identified with ductile materials such as metals. In field-scale rock masses, structural discontinuities exist in the rock indicating that failure has taken place. Since the rock has not fallen apart, contrary to expectation of brittle behavior, clearly elasticity theory is not the last word.
In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.
In astrophysics, the Chandrasekhar virial equations are a hierarchy of moment equations of the Euler equations, developed by the Indian American astrophysicist Subrahmanyan Chandrasekhar, and the physicist Enrico Fermi and Norman R. Lebovitz.
The Pomeranchuk instability is an instability in the shape of the Fermi surface of a material with interacting fermions, causing Landau’s Fermi liquid theory to break down. It occurs when a Landau parameter in Fermi liquid theory has a sufficiently negative value, causing deformations of the Fermi surface to be energetically favourable. It is named after the Soviet physicist Isaak Pomeranchuk.































