Fringe search

Last updated

In computer science, fringe search is a graph search algorithm that finds the least-cost path from a given initial node to one goal node.

Contents

In essence, fringe search is a middle ground between A* and the iterative deepening A* variant (IDA*).

If g(x) is the cost of the search path from the first node to the current, and h(x) is the heuristic estimate of the cost from the current node to the goal, then ƒ(x) = g(x) + h(x), and h* is the actual path cost to the goal. Consider IDA*, which does a recursive left-to-right depth-first search from the root node, stopping the recursion once the goal has been found or the nodes have reached a maximum value ƒ. If no goal is found in the first threshold ƒ, the threshold is then increased and the algorithm searches again. I.E. It iterates on the threshold.

There are three major inefficiencies with IDA*. First, IDA* will repeat states when there are multiple (sometimes non-optimal) paths to a goal node - this is often solved by keeping a cache of visited states. IDA* thus altered is denoted as memory-enhanced IDA* (ME-IDA*), since it uses some storage. Furthermore, IDA* repeats all previous operations in a search when it iterates in a new threshold, which is necessary to operate with no storage. By storing the leaf nodes of a previous iteration and using them as the starting position of the next, IDA*'s efficiency is significantly improved (otherwise, in the last iteration it would always have to visit every node in the tree).

Fringe search implements these improvements on IDA* by making use of a data structure that is more or less two lists to iterate over the frontier or fringe of the search tree. One list now, stores the current iteration, and the other list later stores the immediate next iteration. So from the root node of the search tree, now will be the root and later will be empty. Then the algorithm takes one of two actions: If ƒ(head) is greater than the current threshold, remove head from now and append it to the end of later; i.e. save head for the next iteration. Otherwise, if ƒ(head) is less than or equal to the threshold, expand head and discard head, consider its children, adding them to the beginning of now. At the end of an iteration, the threshold is increased, the later list becomes the now list, and later is emptied.

An important difference here between fringe and A* is that the contents of the lists in fringe do not necessarily have to be sorted - a significant gain over A*, which requires the often expensive maintenance of order in its open list. Unlike A*, however, fringe will have to visit the same nodes repeatedly, but the cost for each such visit is constant compared to the worst-case logarithmic time of sorting the list in A*.

Pseudocode

Implementing both lists in one doubly linked list, where nodes that precede the current node are the later portion and all else are the now list. Using an array of pre-allocated nodes in the list for each node in the grid, access time to nodes in the list is reduced to a constant. Similarly, a marker array allows lookup of a node in the list to be done in constant time. g is stored as a hash-table, and a last marker array is stored for constant-time lookup of whether or not a node has been visited before and if a cache entry is valid.

init(start,goal)fringeF=scacheC[start]=(0,null)flimit=h(start)found=falsewhile(found==false)AND(Fnotempty)fmin=∞fornodeinF,fromlefttoright(g,parent)=C[node]f=g+h(node)iff>flimitfmin=min(f,fmin)continueifnode==goalfound=truebreakforchildinchildren(node),fromrighttoleftg_child=g+cost(node,child)ifC[child]!=null(g_cached,parent)=C[child]ifg_child>=g_cachedcontinueifchildinFremovechildfromFinsertchildinFpastnodeC[child]=(g_child,node)removenodefromFflimit=fminifreachedgoal==truereverse_path(goal)

Reverse pseudo-code.

reverse_path(node)(g,parent)=C[node]ifparent!=nullreverse_path(parent)printnode

Experiments

When tested on grid-based environments typical of computer games including impassable obstacles, fringe outperformed A* by some 10 percent to 40 percent, depending on use of tiles or octiles. Possible further improvements include use of a data structure that lends itself more easily to caches.

Related Research Articles

<span class="mw-page-title-main">AVL tree</span> Self-balancing binary search tree

In computer science, an AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.

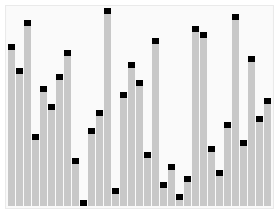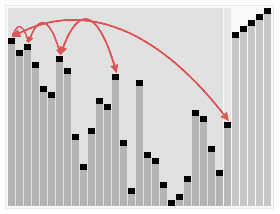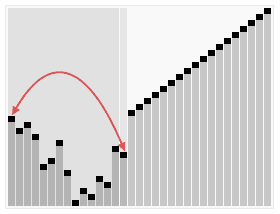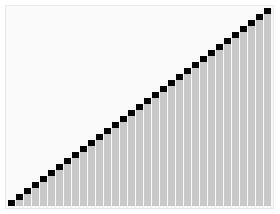
<span class="mw-page-title-main">Heapsort</span> A sorting algorithm which uses the heap data structure

In computer science, heapsort is a comparison-based sorting algorithm which can be thought of as "an implementation of selection sort using the right data structure." Like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to efficiently find the largest element in each step.

<span class="mw-page-title-main">Insertion sort</span> Sorting algorithm

Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:

In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes which together represent a sequence. In its most basic form, each node contains data, and a reference to the next node in the sequence. This structure allows for efficient insertion or removal of elements from any position in the sequence during iteration. More complex variants add additional links, allowing more efficient insertion or removal of nodes at arbitrary positions. A drawback of linked lists is that data access time is linear in respect to the number of nodes in the list. Because nodes are serially linked, accessing any node requires that the prior node be accessed beforehand. Faster access, such as random access, is not feasible. Arrays have better cache locality compared to linked lists.

In computer science, a red–black tree is a self-balancing binary search tree data structure noted for fast storage and retrieval of ordered information. The nodes in a red-black tree hold an extra "color" bit, often drawn as red and black, which help ensure that the tree is always approximately balanced.

A splay tree is a binary search tree with the additional property that recently accessed elements are quick to access again. Like self-balancing binary search trees, a splay tree performs basic operations such as insertion, look-up and removal in O(log n) amortized time. For random access patterns drawn from a non-uniform random distribution, their amortized time can be faster than logarithmic, proportional to the entropy of the access pattern. For many patterns of non-random operations, also, splay trees can take better than logarithmic time, without requiring advance knowledge of the pattern. According to the unproven dynamic optimality conjecture, their performance on all access patterns is within a constant factor of the best possible performance that could be achieved by any other self-adjusting binary search tree, even one selected to fit that pattern. The splay tree was invented by Daniel Sleator and Robert Tarjan in 1985.

<span class="mw-page-title-main">Dijkstra's algorithm</span> Algorithm for finding shortest paths

Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

<span class="mw-page-title-main">Depth-first search</span> Search algorithm

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node and explores as far as possible along each branch before backtracking. Extra memory, usually a stack, is needed to keep track of the nodes discovered so far along a specified branch which helps in backtracking of the graph.

A* is a graph traversal and pathfinding algorithm, which is used in many fields of computer science due to its completeness, optimality, and optimal efficiency. Given a weighted graph, a source node and a goal node, the algorithm finds the shortest path from source to goal.

In computer science, iterative deepening search or more specifically iterative deepening depth-first search is a state space/graph search strategy in which a depth-limited version of depth-first search is run repeatedly with increasing depth limits until the goal is found. IDDFS is optimal, meaning that it finds the shallowest goal. Since it visits all the nodes in the search tree down to depth before visiting any nodes at depth , the cumulative order in which nodes are first visited is effectively the same as in breadth-first search. However, IDDFS uses much less memory.

In computer science, tree traversal is a form of graph traversal and refers to the process of visiting each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well.

<span class="mw-page-title-main">Radix tree</span> Data structure

In computer science, a radix tree is a data structure that represents a space-optimized trie in which each node that is the only child is merged with its parent. The result is that the number of children of every internal node is at most the radix r of the radix tree, where r = 2x for some integer x ≥ 1. Unlike regular trees, edges can be labeled with sequences of elements as well as single elements. This makes radix trees much more efficient for small sets and for sets of strings that share long prefixes.

Iterative deepening A* (IDA*) is a graph traversal and path search algorithm that can find the shortest path between a designated start node and any member of a set of goal nodes in a weighted graph. It is a variant of iterative deepening depth-first search that borrows the idea to use a heuristic function to conservatively estimate the remaining cost to get to the goal from the A* search algorithm. Since it is a depth-first search algorithm, its memory usage is lower than in A*, but unlike ordinary iterative deepening search, it concentrates on exploring the most promising nodes and thus does not go to the same depth everywhere in the search tree. Unlike A*, IDA* does not utilize dynamic programming and therefore often ends up exploring the same nodes many times.

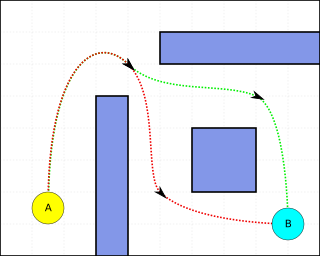
<span class="mw-page-title-main">Pathfinding</span> Plotting by a computer application

Pathfinding or pathing is the search, by a computer application, for the shortest route between two points. It is a more practical variant on solving mazes. This field of research is based heavily on Dijkstra's algorithm for finding the shortest path on a weighted graph.

Bidirectional search is a graph search algorithm that finds a shortest path from an initial vertex to a goal vertex in a directed graph. It runs two simultaneous searches: one forward from the initial state, and one backward from the goal, stopping when the two meet. The reason for this approach is that in many cases it is faster: for instance, in a simplified model of search problem complexity in which both searches expand a tree with branching factor b, and the distance from start to goal is d, each of the two searches has complexity O(bd/2) (in Big O notation), and the sum of these two search times is much less than the O(bd) complexity that would result from a single search from the beginning to the goal.

<span class="mw-page-title-main">Recursion (computer science)</span> Use of functions that call themselves

In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.

The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.

In computer science, graph traversal refers to the process of visiting each vertex in a graph. Such traversals are classified by the order in which the vertices are visited. Tree traversal is a special case of graph traversal.

In computer science, specifically in algorithms related to pathfinding, a heuristic function is said to be admissible if it never overestimates the cost of reaching the goal, i.e. the cost it estimates to reach the goal is not higher than the lowest possible cost from the current point in the path. In other words, it should act as a lower bound.

Theta* is an any-angle path planning algorithm that is based on the A* search algorithm. It can find near-optimal paths with run times comparable to those of A*.

In computer science, anytime A* is a family of variants of the A* search algorithm. Like other anytime algorithms, it has a flexible time cost, can return a valid solution to a pathfinding or graph traversal problem even if it is interrupted before it ends, by generating a fast, non-optimal solution before progressively optimizing it. This ability to quickly generate solutions has made it attractive to Search-base sites and AI designs.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.