 | This article needs additional citations for verification .(March 2015) |
 | This article may be too technical for most readers to understand.(November 2009) |
SMA* or Simplified Memory Bounded A* is a shortest path algorithm based on the A* algorithm. The main advantage of SMA* is that it uses a bounded memory, while the A* algorithm might need exponential memory. All other characteristics of SMA* are inherited from A*.
SMA* has the following properties
The implementation of Simple memory bounded A* is very similar to that of A*; the only difference is that nodes with the highest f-cost are pruned from the queue when there isn't any space left. Because those nodes are deleted, simple memory bounded A* has to remember the f-cost of the best forgotten child of the parent node. When it seems that all explored paths are worse than such a forgotten path, the path is regenerated. [1]
Pseudo code:
functionsimplememoryboundedA*-star(problem):pathqueue:setofnodes,orderedbyf-cost;beginqueue.insert(problem.root-node);whileTruedobeginifqueue.empty()thenreturnfailure;//there is no solution that fits in the given memorynode:=queue.begin();// min-f-cost-nodeifproblem.is-goal(node)thenreturnsuccess;s:=next-successor(node)if!problem.is-goal(s)&&depth(s)==max_depththenf(s):=inf;// there is no memory left to go past s, so the entire path is uselesselsef(s):=max(f(node),g(s)+h(s));// f-value of the successor is the maximum of// f-value of the parent and // heuristic of the successor + path length to the successorendififnomoresuccessorsthenupdatef-costofnodeandthoseofitsancestorsifneededifnode.successors⊆queuethenqueue.remove(node);// all children have already been added to the queue via a shorter wayifmemoryisfullthenbeginbadNode:=shallowestnodewithhighestf-cost;forparentinbadNode.parentsdobeginparent.successors.remove(badNode);ifneededthenqueue.insert(parent);endforendifqueue.insert(s);endwhileendIn computer science, a priority queue is an abstract data type similar to a regular queue or stack abstract data type. Each element in a priority queue has an associated priority. In a priority queue, elements with high priority are served before elements with low priority. In some implementations, if two elements have the same priority, they are served in the same order in which they were enqueued. In other implementations, the order of elements with the same priority is undefined.
A splay tree is a binary search tree with the additional property that recently accessed elements are quick to access again. Like self-balancing binary search trees, a splay tree performs basic operations such as insertion, look-up and removal in O(log n) amortized time. For random access patterns drawn from a non-uniform random distribution, their amortized time can be faster than logarithmic, proportional to the entropy of the access pattern. For many patterns of non-random operations, also, splay trees can take better than logarithmic time, without requiring advance knowledge of the pattern. According to the unproven dynamic optimality conjecture, their performance on all access patterns is within a constant factor of the best possible performance that could be achieved by any other self-adjusting binary search tree, even one selected to fit that pattern. The splay tree was invented by Daniel Sleator and Robert Tarjan in 1985.
The travelling salesman problem (TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.
Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.
A* is a graph traversal and pathfinding algorithm, which is used in many fields of computer science due to its completeness, optimality, and optimal efficiency. Given a weighted graph, a source node and a goal node, the algorithm finds the shortest path from source to goal.
Best-first search is a class of search algorithms, which explores a graph by expanding the most promising node chosen according to a specified rule.
Branch and bound is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution. It is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as mathematical optimization. A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm.
Iterative deepening A* (IDA*) is a graph traversal and path search algorithm that can find the shortest path between a designated start node and any member of a set of goal nodes in a weighted graph. It is a variant of iterative deepening depth-first search that borrows the idea to use a heuristic function to conservatively estimate the remaining cost to get to the goal from the A* search algorithm. Since it is a depth-first search algorithm, its memory usage is lower than in A*, but unlike ordinary iterative deepening search, it concentrates on exploring the most promising nodes and thus does not go to the same depth everywhere in the search tree. Unlike A*, IDA* does not utilize dynamic programming and therefore often ends up exploring the same nodes many times.
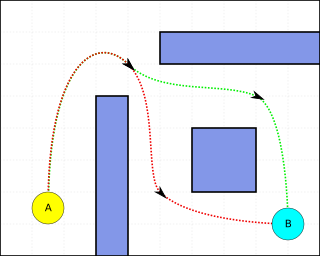
Pathfinding or pathing is the search, by a computer application, for the shortest route between two points. It is a more practical variant on solving mazes. This field of research is based heavily on Dijkstra's algorithm for finding the shortest path on a weighted graph.
Bidirectional search is a graph search algorithm that finds a shortest path from an initial vertex to a goal vertex in a directed graph. It runs two simultaneous searches: one forward from the initial state, and one backward from the goal, stopping when the two meet. The reason for this approach is that in many cases it is faster: for instance, in a simplified model of search problem complexity in which both searches expand a tree with branching factor b, and the distance from start to goal is d, each of the two searches has complexity O(bd/2) (in Big O notation), and the sum of these two search times is much less than the O(bd) complexity that would result from a single search from the beginning to the goal.
In computer science, specifically in algorithms related to pathfinding, a heuristic function is said to be admissible if it never overestimates the cost of reaching the goal, i.e. the cost it estimates to reach the goal is not higher than the lowest possible cost from the current point in the path. In other words, it should act as a lower bound.
In mathematical optimization and computer science, heuristic is a technique designed for problem solving more quickly when classic methods are too slow for finding an exact or approximate solution, or when classic methods fail to find any exact solution in a search space. This is achieved by trading optimality, completeness, accuracy, or precision for speed. In a way, it can be considered a shortcut.
In computer science, B* is a best-first graph search algorithm that finds the least-cost path from a given initial node to any goal node. First published by Hans Berliner in 1979, it is related to the A* search algorithm.
In computer science, fringe search is a graph search algorithm that finds the least-cost path from a given initial node to one goal node.
Any-angle path planning algorithms are pathfinding algorithms that search for a Euclidean shortest path between two points on a grid map while allowing the turns in the path to have any angle. The result is a path that cuts directly through open areas and has relatively few turns. More traditional pathfinding algorithms such as A* either lack in performance or produce jagged, indirect paths.
In computer science, an optimal binary search tree (Optimal BST), sometimes called a weight-balanced binary tree, is a binary search tree which provides the smallest possible search time (or expected search time) for a given sequence of accesses (or access probabilities). Optimal BSTs are generally divided into two types: static and dynamic.
In computer science, anytime A* is a family of variants of the A* search algorithm. Like other anytime algorithms, it has a flexible time cost, can return a valid solution to a pathfinding or graph traversal problem even if it is interrupted before it ends, by generating a fast, non-optimal solution before progressively optimizing it. This ability to quickly generate solutions has made it attractive to Search-base sites and AI designs.
LPA* or Lifelong Planning A* is an incremental heuristic search algorithm based on A*. It was first described by Sven Koenig and Maxim Likhachev in 2001.