Geometric terms of location

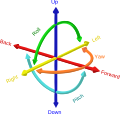
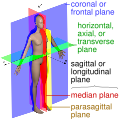
Geometric terms of location describe directions or positions relative to the shape of an object. These terms are used in descriptions of engineering, physics, and other sciences, as well as ordinary day-to-day discourse. ^[1]

Though these terms themselves may be somewhat ambiguous, they are usually used in a context in which their meaning is clear. For example, when referring to a drive shaft it is clear what is meant by axial or radial directions. Or, in a free body diagram, one may similarly infer a sense of orientation by the forces or other vectors represented. ^[1]

Examples

Common geometric terms of location are:

Radial (solid and colored lines) and circumferential roads (dashed and gray lines) in Metro Manila's road network

• Axial – along the center of a round body, or the axis of rotation of a body
• Radial – along a direction pointing along a radius from the center of an object, or perpendicular to a curved path.
• Circumferential (or azimuthal ) – following around a curve or circumference of an object. For instance: the pattern of cells in Taylor–Couette flow varies along the azimuth of the experiment.
• Tangential – intersecting a curve at a point and parallel to the curve at that point.

• Collinear – in the same line
• Parallel – in the same direction.
• Transverse – intersecting at any angle, i.e. not parallel.
• Orthogonal (or perpendicular ) – at a right angle (at the point of intersection).

• Elevation – along a curve from a point on the horizon to the zenith, directly overhead.
• Depression – along a curve from a point on the horizon to the nadir, directly below.

• Vertical – spanning the height of a body.
• Longitudinal – spanning the length of a body.
• Lateral – spanning the width of a body. The distinction between width and length may be unclear out of context.

• Adjacent – next to
• Lineal – following along a given path. The shape of the path is not necessarily straight (compare to linear). For instance, a length of rope might be measured in lineal meters or feet. See arc length.

• Projection / Projected - in architecture, facade sticking out; convex.
• Recession / Recessed - the action of receding; away from an observer; concave.

See also

• 
  Six degrees of freedom
• 
  Anatomical terms of location
• 
  Anatomical plane

References

1. "Geometric Terms and Their Definitions | DREME TE". prek-math-te.stanford.edu. Retrieved 2025-06-20.