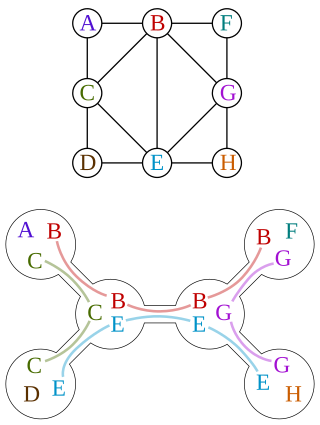
In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to define the treewidth of the graph and speed up solving certain computational problems on the graph.
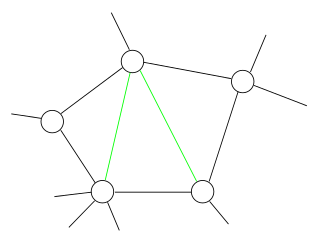
In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.
In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly k are called k-trees, and the graphs with treewidth at most k are called partial k-trees. Many other well-studied graph families also have bounded treewidth.
In graph theory, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.
In computer science, a kernelization is a technique for designing efficient algorithms that achieve their efficiency by a preprocessing stage in which inputs to the algorithm are replaced by a smaller input, called a "kernel". The result of solving the problem on the kernel should either be the same as on the original input, or it should be easy to transform the output on the kernel to the desired output for the original problem.

In graph theory, the clique-width of a graph G is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct G by means of the following 4 operations :
- Creation of a new vertex v with label i (denoted by i(v))
- Disjoint union of two labeled graphs G and H (denoted by )
- Joining by an edge every vertex labeled i to every vertex labeled j (denoted by η(i,j)), where i ≠ j
- Renaming label i to label j (denoted by ρ(i,j))

In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of G is the minimum width of any branch-decomposition of G.
Michael Ralph Fellows AC HFRSNZ MAE is a computer scientist and the Elite Professor of Computer Science in the Department of Informatics at the University of Bergen, Norway as of January 2016.
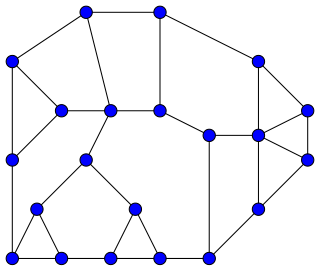
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross, and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.
In graph theory, a partial k-tree is a type of graph, defined either as a subgraph of a k-tree or as a graph with treewidth at most k. Many NP-hard combinatorial problems on graphs are solvable in polynomial time when restricted to the partial k-trees, for bounded values of k.
Jan van Leeuwen is a Dutch computer scientist and emeritus professor of computer science at the Department of Information and Computing Sciences at Utrecht University.
In theoretical computer science, Baker's technique is a method for designing polynomial-time approximation schemes (PTASs) for problems on planar graphs. It is named after Brenda Baker, who announced it in a 1983 conference and published it in the Journal of the ACM in 1994.

Rodney Graham Downey is a New Zealand and Australian mathematician and computer scientist, an emeritus professor in the School of Mathematics and Statistics at Victoria University of Wellington in New Zealand. He is known for his work in mathematical logic and computational complexity theory, and in particular for founding the field of parameterised complexity together with Michael Fellows.
In the study of graph algorithms, Courcelle's theorem is the statement that every graph property definable in the monadic second-order logic of graphs can be decided in linear time on graphs of bounded treewidth. The result was first proved by Bruno Courcelle in 1990 and independently rediscovered by Borie, Parker & Tovey (1992). It is considered the archetype of algorithmic meta-theorems.
The EATCS–IPEC Nerode Prize is a theoretical computer science prize awarded for outstanding research in the area of multivariate algorithmics. It is awarded by the European Association for Theoretical Computer Science and the International Symposium on Parameterized and Exact Computation. The prize was offered for the first time in 2013.
In the parameterized complexity of algorithms, the klam value of a parameterized algorithm is a number that bounds the parameter values for which the algorithm might reasonably be expected to be practical. An algorithm with a higher klam value can be used for a wider range of parameter values than another algorithm with a lower klam value. The klam value was first defined by Downey and Fellows (1999), and has since been used by other researchers in parameterized complexity both as a way of comparing different algorithms to each other and in order to set goals for future algorithmic improvements.
Fedor V. Fomin is a professor of Computer Science at the University of Bergen. He is known for his work in algorithms and graph theory. He received his PhD in 1997 at St. Petersburg State University under Nikolai Nikolaevich Petrov.
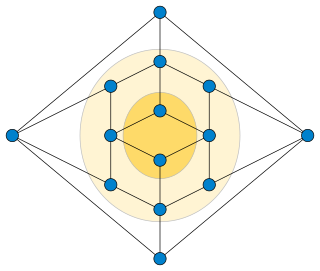
In graph theory, a k-outerplanar graph is a planar graph that has a planar embedding in which the vertices belong to at most concentric layers. The outerplanarity index of a planar graph is the minimum value of for which it is -outerplanar.

In graph theory, the cutwidth of an undirected graph is the smallest integer with the following property: there is an ordering of the vertices of the graph, such that every cut obtained by partitioning the vertices into earlier and later subsets of the ordering is crossed by at most edges. That is, if the vertices are numbered , then for every , the number of edges with and is at most .








