In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary of non-zero length. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubts remain.
In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.
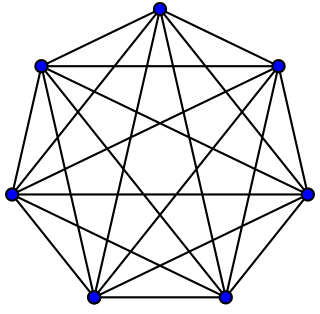
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges.
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.
In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.
In graph theory, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary for graph coloring on a surface of a given genus. For surfaces of genus 0, 1, 2, 3, 4, 5, 6, 7, ..., the required number of colors is 4, 7, 8, 9, 10, 11, 12, 12, .... OEIS: A000934, the chromatic number or Heawood number.
In mathematics, a Kempe chain is a device used mainly in the study of the four colour theorem. Intuitively, it is a connected chain of vertices on a graph with alternating colours.
In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.
In graph theory, Vizing's theorem states that every simple undirected graph may be edge colored using a number of colors that is at most one larger than the maximum degree Δ of the graph. At least Δ colors are always necessary, so the undirected graphs may be partitioned into two classes: "class one" graphs for which Δ colors suffice, and "class two" graphs for which Δ + 1 colors are necessary. A more general version of Vizing's theorem states that every undirected multigraph without loops can be colored with at most Δ+µ colors, where µ is the multiplicity of the multigraph. The theorem is named for Vadim G. Vizing who published it in 1964.
In graph theory, the hypercube graphQn is the graph formed from the vertices and edges of an n-dimensional hypercube. For instance, the cube graph Q3 is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. Qn has 2n vertices, 2n – 1n edges, and is a regular graph with n edges touching each vertex.
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.
In mathematics, the Cheeger constant of a graph is a numerical measure of whether or not a graph has a "bottleneck". The Cheeger constant as a measure of "bottleneckedness" is of great interest in many areas: for example, constructing well-connected networks of computers, card shuffling. The graph theoretical notion originated after the Cheeger isoperimetric constant of a compact Riemannian manifold.
The discharging method is a technique used to prove lemmas in structural graph theory. Discharging is most well known for its central role in the proof of the four color theorem. The discharging method is used to prove that every graph in a certain class contains some subgraph from a specified list. The presence of the desired subgraph is then often used to prove a coloring result.
In graph theory, the crossing numbercr(G) of a graph G is the lowest number of edge crossings of a plane drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero. Determining the crossing number continues to be of great importance in graph drawing, as user studies have shown that drawing graphs with few crossings makes it easier for people to understand the drawing.
A combinatorial map is a combinatorial representation of a graph on an orientable surface. A combinatorial map may also be called a combinatorial embedding, a rotation system, an orientable ribbon graph, a fat graph, or a cyclic graph. More generally, an -dimensional combinatorial map is a combinatorial representation of a graph on an -dimensional orientable manifold.
In combinatorial mathematics, the Albertson conjecture is an unproven relationship between the crossing number and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College, who stated it as a conjecture in 2007; it is one of his many conjectures in graph coloring theory. The conjecture states that, among all graphs requiring colors, the complete graph is the one with the smallest crossing number. Equivalently, if a graph can be drawn with fewer crossings than , then, according to the conjecture, it may be colored with fewer than colors.
In graph theory, the thickness of a graph G is the minimum number of planar graphs into which the edges of G can be partitioned. That is, if there exists a collection of k planar graphs, all having the same set of vertices, such that the union of these planar graphs is G, then the thickness of G is at most k. In other words, the thickness of a graph is the minimum number of planar subgraphs whose union equals to graph G.
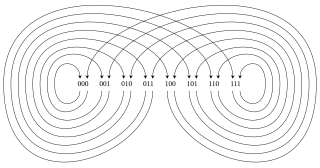
In the mathematical field of graph theory, the queue number of a graph is a graph invariant defined analogously to stack number using first-in first-out (queue) orderings in place of last-in first-out (stack) orderings.
In geometric graph theory, a penny graph is a contact graph of unit circles. It is formed from a collection of unit circles that do not cross each other, by creating a vertex for each circle and an edge for every pair of tangent circles. The circles can be represented physically by pennies, arranged without overlapping on a flat surface, with a vertex for each penny and an edge for each two pennies that touch.
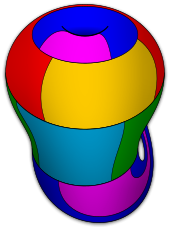
The Earth–Moon problem is an unsolved problem on graph coloring in mathematics. It is an extension of the planar map coloring problem, and was posed by Gerhard Ringel in 1959. An intuitive form of the problem asks how many colors are needed to color political maps of the Earth and Moon, in a hypothetical future where each Earth country has a Moon colony which must be given the same color. In mathematical terms, it seeks the chromatic number of biplanar graphs. It is known that this number is at least 9 and at most 12.
