In geometry, a hendecagrammic prism is a star polyhedron made from two identical regular hendecagrams connected by squares. The related hendecagrammic antiprisms are made from two identical regular hendecagrams connected by equilateral triangles.
There are 4 hendecagrammic uniform prisms, and 6 hendecagrammic uniform antiprisms. The prisms are constructed by 4.4.11/q vertex figures, 
Coxeter diagram. The hendecagrammic bipyramids, duals to the hendecagrammic prisms are also given.
| Symmetry | Prisms | |||
|---|---|---|---|---|
| D11h [2,11] (*2.2.11) |  4.4.11/2  |  4.4.11/3  |  4.4.11/4  |  4.4.11/5  |
| D11h [2,11] (*2.2.11) |    |   |   |   |
The antiprisms with 3.3.3.3.11/q vertex figures, 
. Uniform antiprisms exist for p/q>3/2, [1] and are called crossed for p/q<2. For hendecagonal antiprism, two crossed antiprisms can not be constructed as uniform (with equilateral triangles): 11/8, and 11/9.
| Symmetry | Antiprisms | Crossed- antiprisms | ||
|---|---|---|---|---|
| D11h [2,11] (*2.2.11) |  3.3.3.11/2 |  3.3.3.11/4 |  3.3.3.11/6 3.3.3.-11/5  | Nonuniform 3.3.3.11/8 3.3.3.-11/3 |
| D11d [2+,11] (2*11) |  3.3.3.11/3 |  3.3.3.11/5 |  3.3.3.11/7 3.3.3.-11/4  | Nonuniform 3.3.3.11/9 3.3.3.-11/2 |
The hendecagrammic trapezohedra are duals to the hendecagrammic antiprisms.
| Symmetry | Trapezohedra | ||
|---|---|---|---|
| D11h [2,11] (*2.2.11) |   |  |  |
| D11d [2+,11] (2*11) |  |  |   |
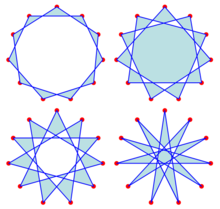
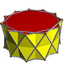
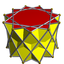
In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies of an n-sided polygon, connected by an alternating band of 2n triangles. They are represented by the Conway notation An.
In geometry, an octahedron is a polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. Many types of irregular octahedra also exist, including both convex and non-convex shapes.
In geometry, the rhombicuboctahedron is an Archimedean solid with 26 faces, consisting of 8 equilateral triangles and 18 squares. It was named by Johannes Kepler in his 1618 Harmonices Mundi, being short for truncated cuboctahedral rhombus, with cuboctahedral rhombus being his name for a rhombic dodecahedron.
A deltahedron is a polyhedron whose faces are all equilateral triangles. The deltahedron is named by Martyn Cundy, after the Greek capital letter delta resembling a triangular shape Δ. The deltahedron can be categorized by the property of convexity. There are eight convex deltahedra, which can be used in the applications of chemistry as in the polyhedral skeletal electron pair theory and chemical compounds. Omitting the convex property leaves the results in infinitely many deltahedrons alongside its subclasses recognition.
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general n-polytope is sliced off.
In geometry, the term semiregular polyhedron is used variously by different authors.
In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruent. Uniform polyhedra may be regular, quasi-regular, or semi-regular. The faces and vertices don't need to be convex, so many of the uniform polyhedra are also star polyhedra.
In geometry, a triangular prism or trigonal prism is a prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a right triangular prism. A right triangular prism may be both semiregular and uniform.
In geometry, a snub polyhedron is a polyhedron obtained by performing a snub operation: alternating a corresponding omnitruncated or truncated polyhedron, depending on the definition. Some, but not all, authors include antiprisms as snub polyhedra, as they are obtained by this construction from a degenerate "polyhedron" with only two faces.
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both.
In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms. All have their vertices in parallel planes and are therefore prismatoids.
In geometry, a hemipolyhedron is a uniform star polyhedron some of whose faces pass through its center. These "hemi" faces lie parallel to the faces of some other symmetrical polyhedron, and their count is half the number of faces of that other polyhedron – hence the "hemi" prefix.
In geometry, an omnitruncated polyhedron is a truncated quasiregular polyhedron. When they are alternated, they produce the snub polyhedra.
In geometry, there are seven uniform and uniform dual polyhedra named as ditrigonal.