In geometry, a polyhedron is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices.
In geometry, a polygon is a plane figure made up of line segments connected to form a closed polygonal chain.

In geometry, a prism is a polyhedron comprising an n-sided polygon base, a second base which is a translated copy of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.

In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple or star polygons.
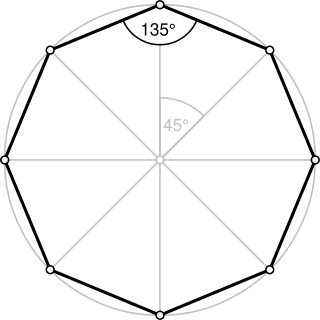
In geometry, an octagon is an eight-sided polygon or 8-gon.

In geometry, the Schläfli symbol is a notation of the form that defines regular polytopes and tessellations.
In geometry, a polytope or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in the same or reverse order, and with the same angles between corresponding faces.

In geometry, a hendecagon or 11-gon is an eleven-sided polygon.
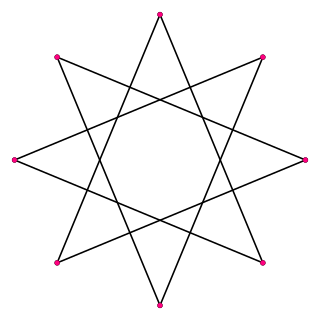
In geometry, an octagram is an eight-angled star polygon.
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. A pyramid is a conic solid with a polygonal base. Many types of pyramids can be found by determining the shape of bases, either by based on a regular polygon or by cutting off the apex. It can be generalized into higher dimensions, known as hyperpyramid. All pyramids are self-dual.

In geometry, a vertex configuration is a shorthand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron.
5 (five) is a number, numeral and digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number.

In mathematics, a hexadecagon is a sixteen-sided polygon.

In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. Here, "vertex-transitive" means that it has symmetries taking every vertex to every other vertex; the same must also be true within each lower-dimensional face of the polytope. In two dimensions a stronger definition is used: only the regular polygons are considered as uniform, disallowing polygons that alternate between two different lengths of edges.
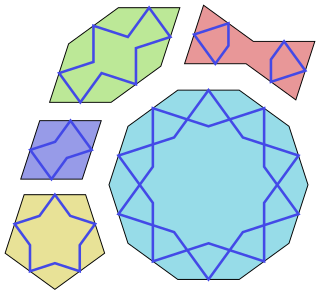
Girihtiles are a set of five tiles that were used in the creation of Islamic geometric patterns using strapwork (girih) for decoration of buildings in Islamic architecture. They have been used since about the year 1200 and their arrangements found significant improvement starting with the Darb-i Imam shrine in Isfahan in Iran built in 1453.

Girih are decorative Islamic geometric patterns used in architecture and handicraft objects, consisting of angled lines that form an interlaced strapwork pattern.
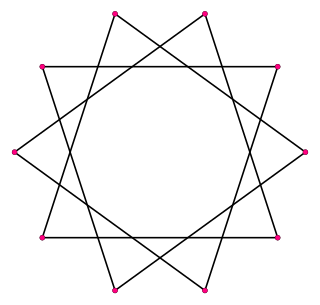
In geometry, a decagram is a 10-point star polygon. There is one regular decagram, containing the vertices of a regular decagon, but connected by every third point. Its Schläfli symbol is {10/3}.

Islamic geometric patterns are one of the major forms of Islamic ornament, which tends to avoid using figurative images, as it is forbidden to create a representation of an important Islamic figure according to many holy scriptures.

In geometry, a dodecagram is a star polygon or compound with 12 vertices. There is one regular dodecagram polygon. There are also 4 regular compounds {12/2},{12/3},{12/4}, and {12/6}.

The Topkapı Scroll is a Timurid dynasty patterned scroll in the collection of the Topkapı Palace museum.