Ex-tangential quadrilateral

Last updated November 15, 2024

In Euclidean geometry, an ex-tangential quadrilateral is a convex quadrilateral where the extensions of all four sides are tangent to a circle outside the quadrilateral.^[1] It has also been called an exscriptible quadrilateral.^[2] The circle is called its excircle, its radius the exradius and its center the excenter ( $E$ in the figure). The excenter lies at the intersection of six angle bisectors. These are the internal angle bisectors at two opposite vertex angles, the external angle bisectors (supplementary angle bisectors) at the other two vertex angles, and the external angle bisectors at the angles formed where the extensions of opposite sides intersect (see the figure to the right, where four of these six are dotted line segments). The ex-tangential quadrilateral is closely related to the tangential quadrilateral (where the four sides are tangent to a circle).

Another name for an excircle is an escribed circle,^[3] but that name has also been used for a circle tangent to one side of a convex quadrilateral and the extensions of the adjacent two sides. In that context all convex quadrilaterals have four escribed circles, but they can at most have one excircle.^[4]

Special cases

Kites are examples of ex-tangential quadrilaterals. Parallelograms (which include squares, rhombi, and rectangles) can be considered ex-tangential quadrilaterals with infinite exradius since they satisfy the characterizations in the next section, but the excircle cannot be tangent to both pairs of extensions of opposite sides (since they are parallel).^[4] Convex quadrilaterals whose side lengths form an arithmetic progression are always ex-tangential as they satisfy the characterization below for adjacent side lengths.

Characterizations

A convex quadrilateral is ex-tangential if and only if there are six concurrent angles bisectors. These are the internal angle bisectors at two opposite vertex angles, the external angle bisectors at the other two vertex angles, and the external angle bisectors at the angles formed where the extensions of opposite sides intersect.^[4]

For the purpose of calculation, a more useful characterization is that a convex quadrilateral with successive sides $a, b, c, d$ is ex-tangential if and only if the sum of two adjacent sides is equal to the sum of the other two sides. This is possible in two different ways:

a+b=c+d

or

a+d=b+c.

This was proved by Jakob Steiner in 1846.^[5] In the first case, the excircle is outside the biggest of the vertices $A$ or $C$ , whereas in the second case it is outside the biggest of the vertices $B$ or $D$ , provided that the sides of the quadrilateral $ABCD$ are

a=|AB|,\ b=|BC|,\ c=|CD|,\ d=|DA|.

A way of combining these characterizations regarding the sides is that the absolute values of the differences between opposite sides are equal for the two pairs of opposite sides,^[4]

|a-c|=|b-d|.

These equations are closely related to the Pitot theorem for tangential quadrilaterals, where the sums of opposite sides are equal for the two pairs of opposite sides.

Urquhart's theorem

If opposite sides in a convex quadrilateral $ABCD$ intersect at $E$ and $F$ , then

|AB|+|BC|=|AD|+|DC|\quad \Leftrightarrow \quad |AE|+|EC|=|AF|+|FC|.

The implication to the right is named after L. M. Urquhart (1902–1966) although it was proved long before by Augustus De Morgan in 1841. Daniel Pedoe named it the most elementary theorem in Euclidean geometry since it only concerns straight lines and distances.^[6] That there in fact is an equivalence was proved by Mowaffac Hajja,^[6] which makes the equality to the right another necessary and sufficient condition for a quadrilateral to be ex-tangential.

Comparison with a tangential quadrilateral

A few of the metric characterizations of tangential quadrilaterals (the left column in the table) have very similar counterparts for ex-tangential quadrilaterals (the middle and right column in the table), as can be seen in the table below.^[4] Thus a convex quadrilateral has an incircle or an excircle outside the appropriate vertex (depending on the column) if and only if any one of the five necessary and sufficient conditions below is satisfied.

Incircle	Excircle outside of $A$ or $C$	Excircle outside of $B$ or $D$
$R_{1}+R_{3}=R_{2}+R_{4}$	$R_{1}+R_{2}=R_{3}+R_{4}$	$R_{1}+R_{4}=R_{2}+R_{3}$
$agh+cef=beh+dfg$	$agh+beh=cef+dfg$	$agh+dfg=beh+cef$
${\frac {1}{h_{1}}}+{\frac {1}{h_{3}}}={\frac {1}{h_{2}}}+{\frac {1}{h_{4}}}$	${\frac {1}{h_{1}}}+{\frac {1}{h_{2}}}={\frac {1}{h_{3}}}+{\frac {1}{h_{4}}}$	${\frac {1}{h_{1}}}+{\frac {1}{h_{4}}}={\frac {1}{h_{2}}}+{\frac {1}{h_{3}}}$
$\tan {\frac {x}{2}}\tan {\frac {z}{2}}=\tan {\frac {y}{2}}\tan {\frac {w}{2}}$	$\tan {\frac {x}{2}}\tan {\frac {w}{2}}=\tan {\frac {y}{2}}\tan {\frac {z}{2}}$	$\tan {\frac {x}{2}}\tan {\frac {y}{2}}=\tan {\frac {z}{2}}\tan {\frac {w}{2}}$
$R_{a}R_{c}=R_{b}R_{d}$	$R_{a}R_{b}=R_{c}R_{d}$	$R_{a}R_{d}=R_{b}R_{c}$

The notations in this table are as follows: In a convex quadrilateral $ABCD$ , the diagonals intersect at $P$ .

$R 1, R 2, R 3, R 4$ are the circumradii in triangles $△ ABP, △ BCP, △ CDP, △ DAP$ ;
$h 1, h 2, h 3, h 4$ are the altitudes from $P$ to the sides $a = | AB |$ , $b = | BC |$ , $c = | CD |$ , $d = | DA |$ respectively in the same four triangles;
$e, f, g, h$ are the distances from the vertices $A, B, C, D$ respectively to $P$ ;
$x, y, z, w$ are the angles $∠ ABD, ∠ ADB, ∠ BDC, ∠ DBC$ respectively;
and $R a, R b, R c, R d$ are the radii in the circles externally tangent to the sides $a, b, c, d$ respectively and the extensions of the adjacent two sides for each side.

Area

An ex-tangential quadrilateral $ABCD$ with sides $a, b, c, d$ has area

\displaystyle K={\sqrt {abcd}}\sin {\frac {B+D}{2}}.

Note that this is the same formula as the one for the area of a tangential quadrilateral and it is also derived from Bretschneider's formula in the same way.

Exradius

The exradius for an ex-tangential quadrilateral with consecutive sides $a, b, c, d$ is given by^[4]

r={\frac {K}{|a-c|}}={\frac {K}{|b-d|}}

where $K$ is the area of the quadrilateral. For an ex-tangential quadrilateral with given sides, the exradius is maximum when the quadrilateral is also cyclic (and hence an ex-bicentric quadrilateral). These formulas explain why all parallelograms have infinite exradius.

Ex-bicentric quadrilateral

If an ex-tangential quadrilateral also has a circumcircle, it is called an ex-bicentric quadrilateral.^[1] Then, since it has two opposite supplementary angles, its area is given by

\displaystyle K={\sqrt {abcd}}

which is the same as for a bicentric quadrilateral.

If $x$ is the distance between the circumcenter and the excenter, then^[1]

{\frac {1}{(R-x)^{2}}}+{\frac {1}{(R+x)^{2}}}={\frac {1}{r^{2}}},

where $R, r$ are the circumradius and exradius respectively. This is the same equation as Fuss's theorem for a bicentric quadrilateral. But when solving for $x$ , we must choose the other root of the quadratic equation for the ex-bicentric quadrilateral compared to the bicentric. Hence, for the ex-bicentric we have^[1]

x={\sqrt {R^{2}+r^{2}+r{\sqrt {4R^{2}+r^{2}}}}}.

From this formula it follows that

\displaystyle x>R+r,

which means that the circumcircle and excircle can never intersect each other.

Related Research Articles

In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices $,, and is sometimes denoted as .$

In Euclidean plane geometry, a rectangle is a rectilinear convex polygon or a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.

<span class="mw-page-title-main">Kite (geometry)</span> Quadrilateral symmetric across a diagonal

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

<span class="mw-page-title-main">Bisection</span> Division of something into two equal or congruent parts

In geometry, bisection is the division of something into two equal or congruent parts. Usually it involves a bisecting line, also called a bisector. The most often considered types of bisectors are the segment bisector, a line that passes through the midpoint of a given segment, and the angle bisector, a line that passes through the apex of an angle . In three-dimensional space, bisection is usually done by a bisecting plane, also called the bisector.

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

<span class="mw-page-title-main">Rhombus</span> Quadrilateral with sides of equal length

In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle, and the latter sometimes refers specifically to a rhombus with a 45° angle.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

<span class="mw-page-title-main">Concyclic points</span> Points on a common circle

In geometry, a set of points are said to be concyclic if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic polygon, and the circle is called its circumscribing circle or circumcircle. All concyclic points are equidistant from the center of the circle.

In Euclidean geometry, a square is a regular quadrilateral, which means that it has four straight sides of equal length and four equal angles. It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°). A square with vertices ABCD would be denoted $ABCD .$

In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name. When the semiperimeter occurs as part of a formula, it is typically denoted by the letter $s$ .

In geometry, lines in a plane or higher-dimensional space are concurrent if they intersect at a single point.

In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".

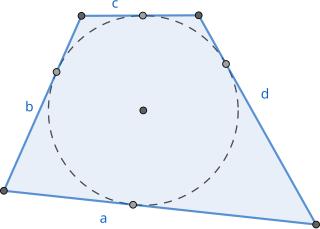
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all can be tangent to a single circle within the quadrilateral. This circle is called the incircle of the quadrilateral or its inscribed circle, its center is the incenter and its radius is called the inradius. Since these quadrilaterals can be drawn surrounding or circumscribing their incircles, they have also been called circumscribable quadrilaterals, circumscribing quadrilaterals, and circumscriptible quadrilaterals. Tangential quadrilaterals are a special case of tangential polygons.

In Euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point $P$ is perpendicular to the radius to that point, theorems involving tangent lines often involve radial lines and orthogonal circles.

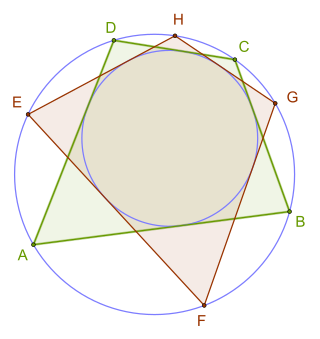
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. The radii and centers of these circles are called inradius and circumradius, and incenter and circumcenter respectively. From the definition it follows that bicentric quadrilaterals have all the properties of both tangential quadrilaterals and cyclic quadrilaterals. Other names for these quadrilaterals are chord-tangent quadrilateral and inscribed and circumscribed quadrilateral. It has also rarely been called a double circle quadrilateral and double scribed quadrilateral.

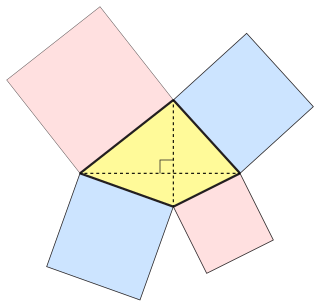
In Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal (perpendicular) to each other.

In Euclidean geometry, a tangential trapezoid, also called a circumscribed trapezoid, is a trapezoid whose four sides are all tangent to a circle within the trapezoid: the incircle or inscribed circle. It is the special case of a tangential quadrilateral in which at least one pair of opposite sides are parallel. As for other trapezoids, the parallel sides are called the bases and the other two sides the legs. The legs can be equal, but they don't have to be.

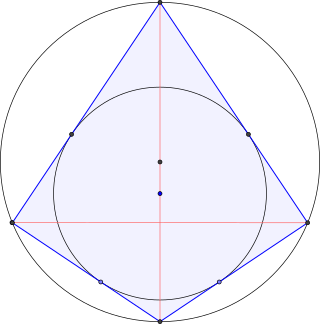
In Euclidean geometry, a right kite is a kite that can be inscribed in a circle. That is, it is a kite with a circumcircle. Thus the right kite is a convex quadrilateral and has two opposite right angles. If there are exactly two right angles, each must be between sides of different lengths. All right kites are bicentric quadrilaterals, since all kites have an incircle. One of the diagonals divides the right kite into two right triangles and is also a diameter of the circumcircle.

In plane geometry, an extended side or sideline of a polygon is the line that contains one side of the polygon. The extension of a finite side into an infinite line arises in various contexts.

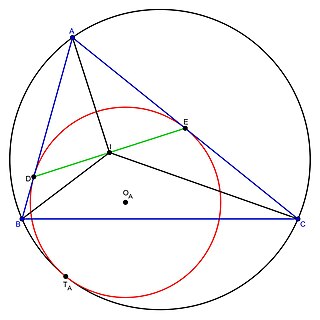
In plane geometry, a mixtilinear incircle of a triangle is a circle which is tangent to two of its sides and internally tangent to its circumcircle. The mixtilinear incircle of a triangle tangent to the two sides containing vertex $is called the -mixtilinear incircle. Every triangle has three unique mixtilinear incircles, one corresponding to each vertex.$

References

1 2 3 4 Radic, Mirko; Kaliman, Zoran and Kadum, Vladimir, "A condition that a tangential quadrilateral is also a chordal one", Mathematical Communications, 12 (2007) pp. 33–52.
↑ Bogomolny, Alexander, "Inscriptible and Exscriptible Quadrilaterals", Interactive Mathematics Miscellany and Puzzles, . Accessed 2011-08-18.
↑ K. S. Kedlaya, Geometry Unbound, 2006
1 2 3 4 5 6 Josefsson, Martin, Similar Metric Characterizations of Tangential and Extangential Quadrilaterals, Forum Geometricorum Volume 12 (2012) pp. 63-77 Archived 2022-01-16 at the Wayback Machine
↑ F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991, p. 318.
1 2 Hajja, Mowaffaq, A Very Short and Simple Proof of “The Most Elementary Theorem” of Euclidean Geometry, Forum Geometricorum Volume 6 (2006) pp. 167–169 Archived 2021-11-19 at the Wayback Machine

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Radic-1] 1 2 3 4 Radic, Mirko; Kaliman, Zoran and Kadum, Vladimir, "A condition that a tangential quadrilateral is also a chordal one", Mathematical Communications, 12 (2007) pp. 33–52.

[2] Bogomolny, Alexander, "Inscriptible and Exscriptible Quadrilaterals", Interactive Mathematics Miscellany and Puzzles, . Accessed 2011-08-18.

[3] K. S. Kedlaya, Geometry Unbound, 2006

[Josefsson-4] 1 2 3 4 5 6 Josefsson, Martin, Similar Metric Characterizations of Tangential and Extangential Quadrilaterals, Forum Geometricorum Volume 12 (2012) pp. 63-77 Archived 2022-01-16 at the Wayback Machine

[5] F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991, p. 318.

[Hajja-6] 1 2 Hajja, Mowaffaq, A Very Short and Simple Proof of “The Most Elementary Theorem” of Euclidean Geometry, Forum Geometricorum Volume 6 (2006) pp. 167–169 Archived 2021-11-19 at the Wayback Machine

[1]

[2]

[3]

[4]

[5]

[6]