
The Mandelbrot set is a two dimensional set with a relatively simple definition that exhibits great complexity, especially as it is magnified. It is popular for its aesthetic appeal and fractal structures. The set is defined in the complex plane as complex numbers for which the function does not diverge to infinity when iterated starting at , i.e., for which the sequence , , etc., remains bounded in absolute value.
In geometry, a polygon is a plane figure made up of line segments connected to form a closed polygonal chain.

In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

A shape or figure is a graphical representation of an object or its external boundary, outline, or external surface, as opposed to other properties such as color, texture, or material type. A plane shape or plane figure is constrained to lie on a plane, in contrast to solid 3D shapes. A two-dimensional shape or two-dimensional figure may lie on a more general curved surface.

In topology, the Jordan curve theorem asserts that every Jordan curve divides the plane into an "interior" region bounded by the curve and an "exterior" region containing all of the nearby and far away exterior points. Every continuous path connecting a point of one region to a point of the other intersects with the curve somewhere. While the theorem seems intuitively obvious, it takes some ingenuity to prove it by elementary means. "Although the JCT is one of the best known topological theorems, there are many, even among professional mathematicians, who have never read a proof of it.". More transparent proofs rely on the mathematical machinery of algebraic topology, and these lead to generalizations to higher-dimensional spaces.

Solid modeling is a consistent set of principles for mathematical and computer modeling of three-dimensional shapes (solids). Solid modeling is distinguished from related areas of geometric modeling and computer graphics, such as 3D modeling, by its emphasis on physical fidelity. Together, the principles of geometric and solid modeling form the foundation of 3D-computer-aided design and in general support the creation, exchange, visualization, animation, interrogation, and annotation of digital models of physical objects.

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes.

In geometry, a straight skeleton is a method of representing a polygon by a topological skeleton. It is similar in some ways to the medial axis but differs in that the skeleton is composed of straight line segments, while the medial axis of a polygon may involve parabolic curves. However, both are homotopy-equivalent to the underlying polygon.
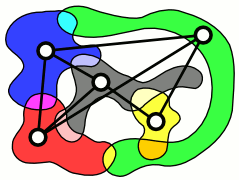
In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types of sets that are used to form an intersection representation of them.

In topological graph theory, an embedding of a graph on a surface is a representation of on in which points of are associated with vertices and simple arcs are associated with edges in such a way that:

A rectilinear polygon is a polygon all of whose sides meet at right angles. Thus the interior angle at each vertex is either 90° or 270°. Rectilinear polygons are a special case of isothetic polygons.

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.

In computational geometry, the visibility polygon or visibility region for a point p in the plane among obstacles is the possibly unbounded polygonal region of all points of the plane visible from p. The visibility polygon can also be defined for visibility from a segment, or a polygon. Visibility polygons are useful in robotics, video games, and in various optimization problems such as the facility location problem and the art gallery problem.

In geometry, a polygon P in the plane is called monotone with respect to a straight line L, if every line orthogonal to L intersects the boundary of P at most twice.

In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain is a curve specified by a sequence of points called its vertices. The curve itself consists of the line segments connecting the consecutive vertices.

In geometry, a convex curve is a plane curve that has a supporting line through each of its points. There are many other equivalent definitions of these curves, going back to Archimedes. Examples of convex curves include the convex polygons, the boundaries of convex sets, and the graphs of convex functions. Important subclasses of convex curves include the closed convex curves, the smooth curves that are convex, and the strictly convex curves, which have the additional property that each supporting line passes through a unique point of the curve.
In geometry, a covering of a polygon is a set of primitive units whose union equals the polygon. A polygon covering problem is a problem of finding a covering with a smallest number of units for a given polygon. This is an important class of problems in computational geometry. There are many different polygon covering problems, depending on the type of polygon being covered. An example polygon covering problem is: given a rectilinear polygon, find a smallest set of squares whose union equals the polygon.
In geometry, a partition of a polygon is a set of primitive units, which do not overlap and whose union equals the polygon. A polygon partition problem is a problem of finding a partition which is minimal in some sense, for example a partition with a smallest number of units or with units of smallest total side-length.

In discrete geometry and computational geometry, the relative convex hull or geodesic convex hull is an analogue of the convex hull for the points inside a simple polygon or a rectifiable simple closed curve.

















