Icositrigon

Regular icositrigon
A regular icositrigon
Type	Regular polygon
Edges and vertices	23
Schläfli symbol	{23}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D23), order 2×23
Internal angle (degrees)	≈164.348°
Properties	Convex, cyclic, equilateral, isogonal, isotoxal
Dual polygon	Self

In geometry, an icositrigon (or icosikaitrigon) or 23-gon is a 23-sided polygon. The icositrigon has the distinction of being the smallest regular polygon that is not neusis constructible.

Regular icositrigon

A regular icositrigon is represented by Schläfli symbol {23}.

A regular icositrigon has internal angles of ${\textstyle {\frac {3780}{23}}}$ degrees, with an area of ${\textstyle A={\frac {23}{4}}a^{2}\cot {\frac {\pi }{23}}=23r^{2}\tan {\frac {\pi }{23}}\simeq 41.8344\,a^{2},}$ where ${\displaystyle a}$ is side length and ${\displaystyle r}$ is the inradius, or apothem.

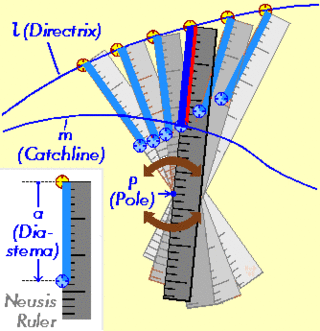
The regular icositrigon is not constructible with a compass and straightedge or angle trisection, ^[1] on account of the number 23 being neither a Fermat nor Pierpont prime. In addition, the regular icositrigon is the smallest regular polygon that is not constructible even with neusis.

Concerning the nonconstructability of the regular icositrigon, A. Baragar (2002) showed it is not possible to construct a regular 23-gon using only a compass and twice-notched straightedge by demonstrating that every point constructible with said method lies in a tower of fields over ${\displaystyle \mathbb {Q} }$ such that ${\displaystyle \mathbb {Q} =K_{0}\subset K_{1}\subset \dots \subset K_{n}=K}$, being a sequence of nested fields in which the degree of the extension at each step is 2, 3, 5, or 6.

Suppose ${\displaystyle \alpha }$ in ${\displaystyle \mathbb {C} }$ is constructible using a compass and twice-notched straightedge. Then ${\displaystyle \alpha }$ belongs to a field ${\displaystyle K}$ that lies in a tower of fields ${\displaystyle \mathbb {Q} =K_{0}\subset K_{1}\subset \dots \subset K_{n}=K}$ for which the index ${\displaystyle [K_{j}:K_{j-1}]}$ at each step is 2, 3, 5, or 6. In particular, if ${\displaystyle N=[K:\mathbb {Q} ]}$, then the only primes dividing ${\displaystyle N}$ are 2, 3, and 5. (Theorem 5.1)

If we can construct the regular p-gon, then we can construct ${\displaystyle \zeta _{p}=e^{\frac {2\pi i}{p}}}$, which is the root of an irreducible polynomial of degree ${\displaystyle p-1}$. By Theorem 5.1, ${\displaystyle \zeta _{p}}$ lies in a field ${\displaystyle K}$ of degree ${\displaystyle N}$ over ${\displaystyle \mathbb {Q} }$, where the only primes that divide ${\displaystyle N}$ are 2, 3, and 5. But ${\displaystyle \mathbb {Q} [\zeta _{p}]}$ is a subfield of ${\displaystyle K}$, so ${\displaystyle p-1}$ divides ${\displaystyle N}$. In particular, for ${\displaystyle p=23}$, ${\displaystyle N}$ must be divisible by 11, and for ${\displaystyle p=29}$, N must be divisible by 7. ^[2]

This result establishes, considering prime-power regular polygons less than the 100-gon, that it is impossible to construct the 23-, 29-, 43-, 47-, 49-, 53-, 59-, 67-, 71-, 79-, 83-, and 89-gons with neusis. But it is not strong enough to decide the cases of the 11-, 25-, 31-, 41-, and 61-gons. Elliot Benjamin and Chip Snyder discovered in 2014 that the regular hendecagon (11-gon) is neusis constructible; the remaining cases are still open. ^[3]

An icositrigon is not origami constructible either, because 23 is not a Pierpont prime, nor a power of two or three. ^[4] It can be constructed using the quadratrix of Hippias, Archimedean spiral, and other auxiliary curves; yet this is true for all regular polygons. ^[5]

Related figures

Below is a table of ten regular icositrigrams, or star 23-gons, labeled with their respective Schläfli symbol {23/q}, 2 ≤ q ≤ 11.

{23/2}	{23/3}	{23/4}	{23/5}	{23/6}
{23/7}	{23/8}	{23/9}	{23/10}	{23/11}

References

1. Tomahawk-nonconstructible n-gons OEIS; https://oeis.org/A048136
2. Arthur Baragar (2002) Constructions Using a Compass and Twice-Notched Straightedge, The American Mathematical Monthly, 109:2, 151-164, doi : 10.1080/00029890.2002.11919848
3. Benjamin, Elliot; Snyder, C. Mathematical Proceedings of the Cambridge Philosophical Society 156.3 (May 2014): 409-424.; https://dx.doi.org/10.1017/S0305004113000753
4. Young Lee, H. (2017) Origami-Constructible Numbers University of Georgia https://getd.libs.uga.edu/pdfs/lee_hwa-young_201712_ma.pdf
5. P. Milici, R. Dawson The equiangular compass December 1st, 2012, The Mathematical Intelligencer, Vol. 34, Issue 4 https://www.researchgate.net/profile/Pietro_Milici2/publication/257393577_The_Equiangular_Compass/links/5d4c687da6fdcc370a8725e0/The-Equiangular-Compass.pdf

External links

• Automated Detection of Interesting Properties in Regular Polygons