| Regular octadecagon | |
|---|---|
 A regular octadecagon | |
| Type | Regular polygon |
| Edges and vertices | 18 |
| Schläfli symbol | {18}, t{9} |
| Coxeter–Dynkin diagrams |     |
| Symmetry group | Dihedral (D18), order 2×18 |
| Internal angle (degrees) | 160° |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | Self |
In geometry, an octadecagon (or octakaidecagon [1] ) or 18-gon is an eighteen-sided polygon. [2]
A regular octadecagon has a Schläfli symbol {18} and can be constructed as a quasiregular truncated enneagon, t{9}, which alternates two types of edges.
As 18 = 2 × 32, a regular octadecagon cannot be constructed using a compass and straightedge. [3] However, it is constructible using neusis, or an angle trisection with a tomahawk.
The following approximate construction is very similar to that of the enneagon, as an octadecagon can be constructed as a truncated enneagon. It is also feasible with exclusive use of compass and straightedge.
|
The regular octadecagon has Dih18 symmetry, order 36. There are 5 subgroup dihedral symmetries: Dih9, (Dih6, Dih3), and (Dih2 Dih1), and 6 cyclic group symmetries: (Z18, Z9), (Z6, Z3), and (Z2, Z1).
These 15 symmetries can be seen in 12 distinct symmetries on the octadecagon. John Conway labels these by a letter and group order. [4] Full symmetry of the regular form is r36 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g18 subgroup has no degrees of freedom but can be seen as directed edges.
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms. [6] In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular octadecagon, m=9, and it can be divided into 36: 4 sets of 9 rhombs. This decomposition is based on a Petrie polygon projection of a 9-cube, with 36 of 4608 faces. The list OEIS: A006245 enumerates the number of solutions as 112018190, including up to 18-fold rotations and chiral forms in reflection.
 |  |  |  |  |
A regular triangle, nonagon, and octadecagon can completely surround a point in the plane, one of 17 different combinations of regular polygons with this property. [7] However, this pattern cannot be extended to an Archimedean tiling of the plane: because the triangle and the nonagon both have an odd number of sides, neither of them can be completely surrounded by a ring alternating the other two kinds of polygon.
The regular octadecagon can tessellate the plane with concave hexagonal gaps. And another tiling mixes in nonagons and octagonal gaps. The first tiling is related to a truncated hexagonal tiling, and the second the truncated trihexagonal tiling.
An octadecagram is an 18-sided star polygon, represented by symbol {18/n}. There are two regular star polygons: {18/5} and {18/7}, using the same points, but connecting every fifth or seventh points. There are also five compounds: {18/2} is reduced to 2{9} or two enneagons, {18/3} is reduced to 3{6} or three hexagons, {18/4} and {18/8} are reduced to 2{9/2} and 2{9/4} or two enneagrams, {18/6} is reduced to 6{3} or 6 equilateral triangles, and finally {18/9} is reduced to 9{2} as nine digons.
| Compounds and star polygons | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Form | Convex polygon | Compounds | Star polygon | Compound | Star polygon | Compound | |||
| Image |  {18/1} = {18} |  {18/2} = 2{9} |  {18/3} = 3{6} |  {18/4} = 2{9/2} |  {18/5} |  {18/6} = 6{3} |  {18/7} |  {18/8} = 2{9/4} |  {18/9} = 9{2} |
| Interior angle | 160° | 140° | 120° | 100° | 80° | 60° | 40° | 20° | 0° |
Deeper truncations of the regular enneagon and enneagrams can produce isogonal (vertex-transitive) intermediate octadecagram forms with equally spaced vertices and two edge lengths. Other truncations form double coverings: t{9/8}={18/8}=2{9/4}, t{9/4}={18/4}=2{9/2}, t{9/2}={18/2}=2{9}. [8]
| Vertex-transitive truncations of enneagon and enneagrams | |||||
|---|---|---|---|---|---|
| Quasiregular | isogonal | Quasiregular Double covering | |||
 t{9}={18} |  |  |  |  |  t{9/8}={18/8} =2{9/4} |
 t{9/5}={18/5} |  |  |  |  |  t{9/4}={18/4} =2{9/2} |
 t{9/7}={18/7} |  |  |  |  |  t{9/2}={18/2} =2{9} |
A regular skew octadecagon is the Petrie polygon for a number of higher-dimensional polytopes, shown in these skew orthogonal projections from Coxeter planes:
| Octadecagonal petrie polygons | |||||||
|---|---|---|---|---|---|---|---|
| A17 | B9 | D10 | E7 | ||||
 17-simplex |  9-orthoplex |  9-cube |  711 |  171 |  321 |  231 |  132 |
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.
In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
In geometry, the truncated cuboctahedron or great rhombicuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.
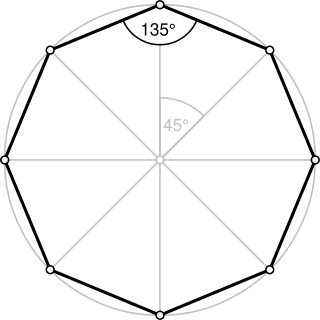
In geometry, an octagon is an eight-sided polygon or 8-gon.
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.
In geometry, a decagon is a ten-sided polygon or 10-gon. The total sum of the interior angles of a simple decagon is 1440°.
In geometry, a nonagon or enneagon is a nine-sided polygon or 9-gon.
In geometry, an icosagon or 20-gon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees.
In geometry, a dodecagon, or 12-gon, is any twelve-sided polygon.
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles. It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ABCD would be denoted ABCD.
In geometry, a triacontagon or 30-gon is a thirty-sided polygon. The sum of any triacontagon's interior angles is 5040 degrees.
In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} .
In geometry, the square tiling, square tessellation or square grid is a regular tiling of the Euclidean plane. It has Schläfli symbol of {4,4}, meaning it has 4 squares around every vertex. Conway called it a quadrille.
In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.
In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.
In geometry, the trihexagonal tiling is one of 11 uniform tilings of the Euclidean plane by regular polygons. It consists of equilateral triangles and regular hexagons, arranged so that each hexagon is surrounded by triangles and vice versa. The name derives from the fact that it combines a regular hexagonal tiling and a regular triangular tiling. Two hexagons and two triangles alternate around each vertex, and its edges form an infinite arrangement of lines. Its dual is the rhombille tiling.
In geometry, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon.
In mathematics, a hexadecagon is a sixteen-sided polygon.
In geometry, an icositetragon or 24-gon is a twenty-four-sided polygon. The sum of any icositetragon's interior angles is 3960 degrees.
In geometry, the truncated trioctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one hexagon, and one hexadecagon (16-sides) on each vertex. It has Schläfli symbol of tr{8,3}.
