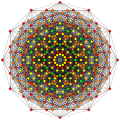
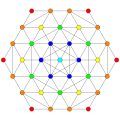
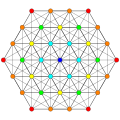
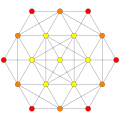
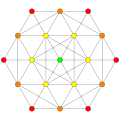
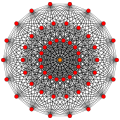
321 |  231 |  132 |
In 7-dimensional geometry, there are 127 uniform polytopes with E7 symmetry. The three simplest forms are the 321, 231, and 132 polytopes, composed of 56, 126, and 576 vertices respectively.
They can be visualized as symmetric orthographic projections in Coxeter planes of the E7 Coxeter group, and other subgroups.