The tomahawk is a tool in geometry for angle trisection, the problem of splitting an angle into three equal parts. The boundaries of its shape include a semicircle and two line segments, arranged in a way that resembles a tomahawk, a Native American axe. [1] [2] The same tool has also been called the shoemaker's knife, [3] but that name is more commonly used in geometry to refer to a different shape, the arbelos (a curvilinear triangle bounded by three mutually tangent semicircles). [4]
The basic shape of a tomahawk consists of a semicircle (the "blade" of the tomahawk), with a line segment the length of the radius extending along the same line as the diameter of the semicircle (the tip of which is the "spike" of the tomahawk), and with another line segment of arbitrary length (the "handle" of the tomahawk) perpendicular to the diameter. In order to make it into a physical tool, its handle and spike may be thickened, as long as the line segment along the handle continues to be part of the boundary of the shape. Unlike a related trisection using a carpenter's square, the other side of the thickened handle does not need to be made parallel to this line segment. [1]
In some sources a full circle rather than a semicircle is used, [5] or the tomahawk is also thickened along the diameter of its semicircle, [6] but these modifications make no difference to the action of the tomahawk as a trisector.
To use the tomahawk to trisect an angle, it is placed with its handle line touching the apex of the angle, with the blade inside the angle, tangent to one of the two rays forming the angle, and with the spike touching the other ray of the angle. One of the two trisecting lines then lies on the handle segment, and the other passes through the center point of the semicircle. [1] [6] If the angle to be trisected is too sharp relative to the length of the tomahawk's handle, it may not be possible to fit the tomahawk into the angle in this way, but this difficulty may be worked around by repeatedly doubling the angle until it is large enough for the tomahawk to trisect it, and then repeatedly bisecting the trisected angle the same number of times as the original angle was doubled. [2]
If the apex of the angle is labeled A, the point of tangency of the blade is B, the center of the semicircle is C, the top of the handle is D, and the spike is E, then triangles △ACD and △ADE are both right triangles with a shared base and equal height, so they are congruent triangles. Because the sides AB and BC of triangle △ABC are respectively a tangent and a radius of the semicircle, they are at right angles to each other and △ABC is also a right triangle; it has the same hypotenuse as △ACD and the same side lengths BC = CD, so again it is congruent to the other two triangles, showing that the three angles formed at the apex are equal. [5] [6]
Although the tomahawk may itself be constructed using a compass and straightedge, [7] and may be used to trisect an angle, it does not contradict Pierre Wantzel's 1837 theorem that arbitrary angles cannot be trisected by compass and unmarked straightedge alone. [8] The reason for this is that placing the constructed tomahawk into the required position is a form of neusis that is not allowed in compass and straightedge constructions. [9]
The inventor of the tomahawk is unknown, [1] [10] but the earliest references to it come from 19th-century France. It dates back at least as far as 1835, when it appeared in a book by Claude Lucien Bergery, Géométrie appliquée à l'industrie, à l'usage des artistes et des ouvriers (3rd edition). [1] Another early publication of the same trisection was made by Henri Brocard in 1877; [11] Brocard in turn attributes its invention to an 1863 memoir by French naval officer Pierre-Joseph Glotin . [12] [13] [14]
In geometry and algebra, a real number is constructible if and only if, given a line segment of unit length, a line segment of length can be constructed with compass and straightedge in a finite number of steps. Equivalently, is constructible if and only if there is a closed-form expression for using only integers and the operations for addition, subtraction, multiplication, division, and square roots.
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a pair of compasses.
Doubling the cube, also known as the Delian problem, is an ancient geometric problem. Given the edge of a cube, the problem requires the construction of the edge of a second cube whose volume is double that of the first. As with the related problems of squaring the circle and trisecting the angle, doubling the cube is now known to be impossible to construct by using only a compass and straightedge, but even in ancient times solutions were known that employed other tools.
Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge and a compass.
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector.
Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square with the area of a circle by using only a finite number of steps with a compass and straightedge. The difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of lines and circles implied the existence of such a square.
The Huzita–Justin axioms or Huzita–Hatori axioms are a set of rules related to the mathematical principles of origami, describing the operations that can be made when folding a piece of paper. The axioms assume that the operations are completed on a plane, and that all folds are linear. These are not a minimal set of axioms but rather the complete set of possible single folds.
In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not. There are infinitely many constructible polygons, but only 31 with an odd number of sides are known.
In the branch of mathematics known as Euclidean geometry, the Poncelet–Steiner theorem is one of several results concerning compass and straightedge constructions having additional restrictions imposed on the traditional rules. This result states that whatever can be constructed by straightedge and compass together can be constructed by straightedge alone, provided that a single circle and its centre are given. This theorem is related to the rusty compass equivalence.
In geometry, a tridecagon or triskaidecagon or 13-gon is a thirteen-sided polygon.
In geometry, an arbelos is a plane region bounded by three semicircles with three apexes such that each corner of each semicircle is shared with one of the others (connected), all on the same side of a straight line that contains their diameters.
Pierre Laurent Wantzel was a French mathematician who proved that several ancient geometric problems were impossible to solve using only compass and straightedge.
In geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle with ruler and compass and this curve as an additional tool. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of construction. There is a variety of such curves and the methods used to construct an angle trisector differ according to the curve. Examples include:
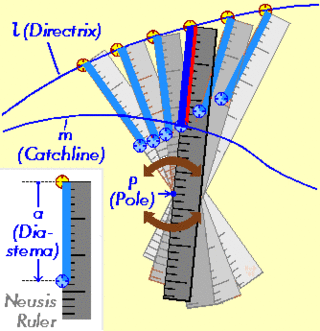
In geometry, the neusis is a geometric construction method that was used in antiquity by Greek mathematicians.
In geometry, an octadecagon or 18-gon is an eighteen-sided polygon.
Émile Michel Hyacinthe Lemoine was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.
In Euclidean geometry, Apollonius' problem is to construct all the circles that are tangent to three given circles. Special cases of Apollonius' problem are those in which at least one of the given circles is a point or line, i.e., is a circle of zero or infinite radius. The nine types of such limiting cases of Apollonius' problem are to construct the circles tangent to:
The Ancient Tradition of Geometric Problems is a book on ancient Greek mathematics, focusing on three problems now known to be impossible if one uses only the straightedge and compass constructions favored by the Greek mathematicians: squaring the circle, doubling the cube, and trisecting the angle. It was written by Wilbur Knorr (1945–1997), a historian of mathematics, and published in 1986 by Birkhäuser. Dover Publications reprinted it in 1993.
Geometric Constructions is a mathematics textbook on constructible numbers, and more generally on using abstract algebra to model the sets of points that can be created through certain types of geometric construction, and using Galois theory to prove limits on the constructions that can be performed. It was written by George E. Martin, and published by Springer-Verlag in 1998 as volume 81 of their Undergraduate Texts in Mathematics book series.
