| Regular tetradecagon | |
|---|---|
 A regular tetradecagon | |
| Type | Regular polygon |
| Edges and vertices | 14 |
| Schläfli symbol | {14}, t{7} |
| Coxeter–Dynkin diagrams |     |
| Symmetry group | Dihedral (D14), order 2×14 |
| Internal angle (degrees) | 154+2/7° |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | Self |
In geometry, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon.
A regular tetradecagon has Schläfli symbol {14} and can be constructed as a quasiregular truncated heptagon, t{7}, which alternates two types of edges.
The area of a regular tetradecagon of side length a is given by
As 14 = 2 × 7, a regular tetradecagon cannot be constructed using a compass and straightedge. [1] However, it is constructible using neusis with use of the angle trisector, [2] or with a marked ruler, [3] as shown in the following two examples.
The regular tetradecagon has Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4 cyclic group symmetries: Z14, Z7, Z2, and Z1.
These 8 symmetries can be seen in 10 distinct symmetries on the tetradecagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order. [4] Full symmetry of the regular form is r28 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g14 subgroup has no degrees of freedom but can be seen as directed edges.
The highest symmetry irregular tetradecagons are d14, an isogonal tetradecagon constructed by seven mirrors which can alternate long and short edges, and p14, an isotoxal tetradecagon, constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular tetradecagon.
 14-cube projection |  84 rhomb dissection |
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms. [5] In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular tetradecagon, m=7, and it can be divided into 21: 3 sets of 7 rhombs. This decomposition is based on a Petrie polygon projection of a 7-cube, with 21 of 672 faces. The list OEIS: A006245 defines the number of solutions as 24698, including up to 14-fold rotations and chiral forms in reflection.
 |  |  |  |  |  |
The regular tetradecagon is used as the shape of some commemorative gold and silver Malaysian coins, the number of sides representing the 14 states of the Malaysian Federation. [6]
A tetradecagram is a 14-sided star polygon, represented by symbol {14/n}. There are two regular star polygons: {14/3} and {14/5}, using the same vertices, but connecting every third or fifth points. There are also three compounds: {14/2} is reduced to 2{7} as two heptagons, while {14/4} and {14/6} are reduced to 2{7/2} and 2{7/3} as two different heptagrams, and finally {14/7} is reduced to seven digons.
A notable application of a fourteen-pointed star is in the flag of Malaysia, which incorporates a yellow {14/6} tetradecagram in the top-right corner, representing the unity of the thirteen states with the federal government.
| Compounds and star polygons | |||||||
|---|---|---|---|---|---|---|---|
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Form | Regular | Compound | Star polygon | Compound | Star polygon | Compound | |
| Image |  {14/1} = {14} |  {14/2} = 2{7}  |  {14/3}   |  {14/4} = 2{7/2}  |  {14/5}  |  {14/6} = 2{7/3} |  {14/7} or 7{2} |
| Internal angle | ≈154.286° | ≈128.571° | ≈102.857° | ≈77.1429° | ≈51.4286° | ≈25.7143° | 0° |
Deeper truncations of the regular heptagon and heptagrams can produce isogonal (vertex-transitive) intermediate tetradecagram forms with equally spaced vertices and two edge lengths. Other truncations can form double covering polygons 2{p/q}, namely: t{7/6}={14/6}=2{7/3}, t{7/4}={14/4}=2{7/2}, and t{7/2}={14/2}=2{7}. [7]
| Isogonal truncations of heptagon and heptagrams | ||||
|---|---|---|---|---|
| Quasiregular | Isogonal | Quasiregular Double covering | ||
 t{7}={14} |  |  |  |  {7/6}={14/6} =2{7/3} |
 t{7/3}={14/3} |  |  |  |  t{7/4}={14/4} =2{7/2} |
 t{7/5}={14/5} |  |  |  |  t{7/2}={14/2} =2{7} |
An isotoxal polygon can be labeled as {pα} with outer most internal angle α, and a star polygon {(p/q)α}, with q is a winding number, and gcd(p,q)=1, q<p. Isotoxal tetradecagons have p=7, and since 7 is prime all solutions, q=1..6, are polygons.
 {7α} |  {(7/2)α} |  {(7/3)α} |  {(7/4)α} |  {(7/5)α} |  {(7/6)α} |
Regular skew tetradecagons exist as Petrie polygon for many higher-dimensional polytopes, shown in these skew orthogonal projections, including:
| Petrie polygons | ||||
|---|---|---|---|---|
| B7 | 2I2(7) (4D) | |||
 7-orthoplex |  7-cube |  7-7 duopyramid |  7-7 duoprism | |
| A13 | D8 | E8 | ||
 13-simplex |  511 |  151 |  421 |  241 |
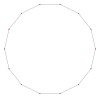
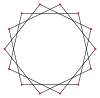
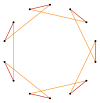
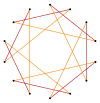
In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
In geometry, a prism is a polyhedron comprising an n-sided polygon base, a second base which is a translated copy of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple or star polygons.
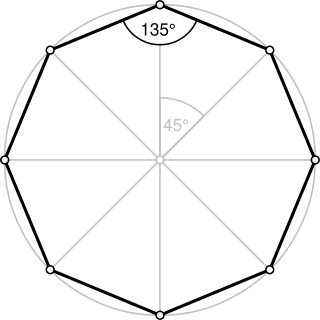
In geometry, an octagon is an eight-sided polygon or 8-gon.
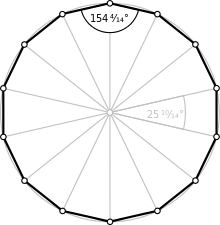
In geometry, a decagon is a ten-sided polygon or 10-gon. The total sum of the interior angles of a simple decagon is 1440°.
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.
In geometry, an icosagon or 20-gon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees.
In geometry, a dodecagon, or 12-gon, is any twelve-sided polygon.
In geometry, a myriagon or 10000-gon is a polygon with 10000 sides. Several philosophers have used the regular myriagon to illustrate issues regarding thought.
In geometry, a polytope or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in the same or reverse order, and with the same angles between corresponding faces.
In geometry, a tridecagon or triskaidecagon or 13-gon is a thirteen-sided polygon.
In geometry, a triacontagon or 30-gon is a thirty-sided polygon. The sum of any triacontagon's interior angles is 5040 degrees.
In Euclidean geometry, an equiangular polygon is a polygon whose vertex angles are equal. If the lengths of the sides are also equal then it is a regular polygon. Isogonal polygons are equiangular polygons which alternate two edge lengths.
In geometry, a polytope or a tiling is isotoxal or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a translation, rotation, and/or reflection that will move one edge to the other while leaving the region occupied by the object unchanged.
In mathematics, a hexadecagon is a sixteen-sided polygon.
In geometry, an octadecagon or 18-gon is an eighteen-sided polygon.
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-transitive.
A megagon or 1,000,000-gon (million-gon) is a polygon with one million sides.
In geometry, an icositetragon or 24-gon is a twenty-four-sided polygon. The sum of any icositetragon's interior angles is 3960 degrees.
In geometry, an infinite skew polygon or skew apeirogon is an infinite 2-polytope with vertices that are not all colinear. Infinite zig-zag skew polygons are 2-dimensional infinite skew polygons with vertices alternating between two parallel lines. Infinite helical polygons are 3-dimensional infinite skew polygons with vertices on the surface of a cylinder.
