In hyperbolic geometry an ideal triangle is a hyperbolic triangle whose three vertices all are ideal points. Ideal triangles are also sometimes called triply asymptotic triangles or trebly asymptotic triangles. The vertices are sometimes called ideal vertices. All ideal triangles are congruent.
Ideal triangles have the following properties:
In the standard hyperbolic plane (a surface where the constant Gaussian curvature is −1) we also have the following properties:
. [2]
Because the ideal triangle is the largest possible triangle in hyperbolic geometry, the measures above are maxima possible for any hyperbolic triangle. This fact is important in the study of δ-hyperbolic space.
In the Poincaré disk model of the hyperbolic plane, an ideal triangle is bounded by three circles which intersect the boundary circle at right angles.
In the Poincaré half-plane model, an ideal triangle is modeled by an arbelos, the figure between three mutually tangent semicircles.
In the Beltrami–Klein model of the hyperbolic plane, an ideal triangle is modeled by a Euclidean triangle that is circumscribed by the boundary circle. Note that in the Beltrami-Klein model, the angles at the vertices of an ideal triangle are not zero, because the Beltrami-Klein model, unlike the Poincaré disk and half-plane models, is not conformal i.e. it does not preserve angles.
 The ideal (∞∞∞) triangle group |  Another ideal tiling |
The real ideal triangle group is the reflection group generated by reflections of the hyperbolic plane through the sides of an ideal triangle. Algebraically, it is isomorphic to the free product of three order-two groups (Schwartz 2001).
In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle. The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex; the shortest segment between the base and apex is the height. The area of a triangle equals one-half the product of height and base length.
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the unit hyperbola. Also, similarly to how the derivatives of sin(t) and cos(t) are cos(t) and –sin(t) respectively, the derivatives of sinh(t) and cosh(t) are cosh(t) and +sinh(t) respectively.
In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
In geometry, inversive geometry is the study of inversion, a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Many difficult problems in geometry become much more tractable when an inversion is applied. Inversion seems to have been discovered by a number of people contemporaneously, including Steiner (1824), Quetelet (1825), Bellavitis (1836), Stubbs and Ingram (1842–3) and Kelvin (1845).
In non-Euclidean geometry, the Poincaré half-plane model is a way of representing the hyperbolic plane using points in the familiar Euclidean plane. Specifically, each point in the hyperbolic plane is represented using a Euclidean point with coordinates whose coordinate is greater than zero, the upper half-plane, and a metric tensor called the Poincaré metric is adopted, in which the local scale is inversely proportional to the coordinate. Points on the -axis, whose coordinate is equal to zero, represent ideal points, which are outside the hyperbolic plane proper.
In geometry, a tractrix is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a pulling point that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of pursuit. It was first introduced by Claude Perrault in 1670, and later studied by Isaac Newton (1676) and Christiaan Huygens (1693).
In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.
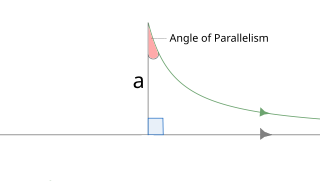
In hyperbolic geometry, angle of parallelism is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.
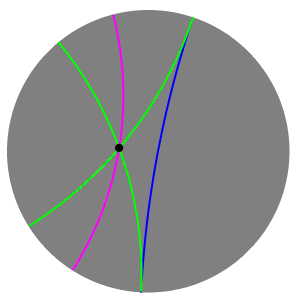
In hyperbolic geometry, two lines are said to be ultraparallel if they do not intersect and are not limiting parallel.
In mathematics, the inverse hyperbolic functions are inverses of the hyperbolic functions, analogous to the inverse circular functions. There are six in common use: inverse hyperbolic sine, inverse hyperbolic cosine, inverse hyperbolic tangent, inverse hyperbolic cosecant, inverse hyperbolic secant, and inverse hyperbolic cotangent. They are commonly denoted by the symbols for the hyperbolic functions, prefixed with arc- or ar-.
In special relativity, the classical concept of velocity is converted to rapidity to accommodate the limit determined by the speed of light. Velocities must be combined by Einstein's velocity-addition formula. For low speeds, rapidity and velocity are almost exactly proportional but, for higher velocities, rapidity takes a larger value, with the rapidity of light being infinite.
In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of hyperbolic geometry in which points are represented by the points in the interior of the unit disk and lines are represented by the chords, straight line segments with ideal endpoints on the boundary sphere.
In hyperbolic geometry, an ideal point, omega point or point at infinity is a well-defined point outside the hyperbolic plane or space. Given a line l and a point P not on l, right- and left-limiting parallels to l through P converge to l at ideal points.
In mathematics, the Bolza surface, alternatively, complex algebraic Bolza curve, is a compact Riemann surface of genus with the highest possible order of the conformal automorphism group in this genus, namely of order 48. The full automorphism group is the semi-direct product of order 96. An affine model for the Bolza surface can be obtained as the locus of the equation
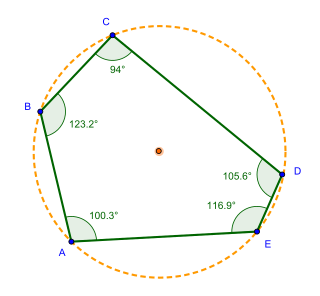
In geometry, a pentagon is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
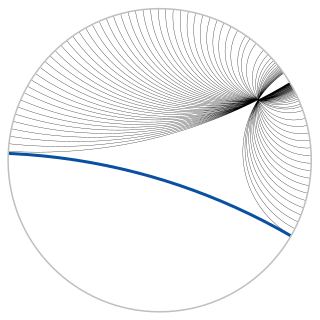
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk that are orthogonal to the unit circle or diameters of the unit circle.
In calculus, the integral of the secant function can be evaluated using a variety of methods and there are multiple ways of expressing the antiderivative, all of which can be shown to be equivalent via trigonometric identities,
In the hyperbolic plane, as in the Euclidean plane, each point can be uniquely identified by two real numbers. Several qualitatively different ways of coordinatizing the plane in hyperbolic geometry are used.
