
A descriptive statistic is a summary statistic that quantitatively describes or summarizes features from a collection of information, while descriptive statistics is the process of using and analysing those statistics. Descriptive statistics is distinguished from inferential statistics by its aim to summarize a sample, rather than use the data to learn about the population that the sample of data is thought to represent. This generally means that descriptive statistics, unlike inferential statistics, is not developed on the basis of probability theory, and are frequently nonparametric statistics. Even when a data analysis draws its main conclusions using inferential statistics, descriptive statistics are generally also presented. For example, in papers reporting on human subjects, typically a table is included giving the overall sample size, sample sizes in important subgroups, and demographic or clinical characteristics such as the average age, the proportion of subjects of each sex, the proportion of subjects with related co-morbidities, etc.
In probability theory and statistics, kurtosis is a measure of the "tailedness" of the probability distribution of a real-valued random variable. Like skewness, kurtosis describes the shape of a probability distribution and there are different ways of quantifying it for a theoretical distribution and corresponding ways of estimating it from a sample from a population. Different measures of kurtosis may have different interpretations.
In probability theory and statistics, a central moment is a moment of a probability distribution of a random variable about the random variable's mean; that is, it is the expected value of a specified integer power of the deviation of the random variable from the mean. The various moments form one set of values by which the properties of a probability distribution can be usefully characterized. Central moments are used in preference to ordinary moments, computed in terms of deviations from the mean instead of from zero, because the higher-order central moments relate only to the spread and shape of the distribution, rather than also to its location.

In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.
In probability theory and statistics, a standardized moment of a probability distribution is a moment that is normalized. The normalization is typically a division by an expression of the standard deviation which renders the moment scale invariant. This has the advantage that such normalized moments differ only in other properties than variability, facilitating e.g. comparison of shape of different probability distributions.

In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by alpha (α) and beta (β), that appear as exponents of the random variable and control the shape of the distribution. The generalization to multiple variables is called a Dirichlet distribution.
In probability theory and statistics, the cumulantsκn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. Any two probability distributions whose moments are identical will have identical cumulants as well, and vice versa.
In mathematics, the moments of a function are quantitative measures related to the shape of the function's graph. If the function represents mass, then the first moment is the center of the mass, and the second moment is the rotational inertia. If the function is a probability distribution, then the first moment is the expected value, the second central moment is the variance, the third standardized moment is the skewness, and the fourth standardized moment is the kurtosis. The mathematical concept is closely related to the concept of moment in physics.
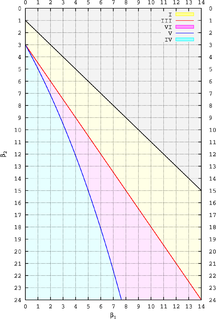
The Pearson distribution is a family of continuous probability distributions. It was first published by Karl Pearson in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics.
This glossary of statistics and probability is a list of definitions of terms and concepts used in the mathematical sciences of statistics and probability, their sub-disciplines, and related fields. For additional related terms, see Glossary of mathematics and Glossary of experimental design.
In mathematics, in the area of statistical analysis, the bispectrum is a statistic used to search for nonlinear interactions.
In statistics, normality tests are used to determine if a data set is well-modeled by a normal distribution and to compute how likely it is for a random variable underlying the data set to be normally distributed.

In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions that is neither a location parameter nor a scale parameter. Such a parameter must affect the shape of a distribution rather than simply shifting it or stretching/shrinking it . For example, "peakedness" refers to how round the main peak is.
In probability and statistics, a natural exponential family (NEF) is a class of probability distributions that is a special case of an exponential family (EF).

In probability and statistics, the log-logistic distribution is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events whose rate increases initially and decreases later, as, for example, mortality rate from cancer following diagnosis or treatment. It has also been used in hydrology to model stream flow and precipitation, in economics as a simple model of the distribution of wealth or income, and in networking to model the transmission times of data considering both the network and the software.
In statistics, L-moments are a sequence of statistics used to summarize the shape of a probability distribution. They are linear combinations of order statistics (L-statistics) analogous to conventional moments, and can be used to calculate quantities analogous to standard deviation, skewness and kurtosis, termed the L-scale, L-skewness and L-kurtosis respectively. Standardised L-moments are called L-moment ratios and are analogous to standardized moments. Just as for conventional moments, a theoretical distribution has a set of population L-moments. Sample L-moments can be defined for a sample from the population, and can be used as estimators of the population L-moments.
In statistics, the Jarque–Bera test is a goodness-of-fit test of whether sample data have the skewness and kurtosis matching a normal distribution. The test is named after Carlos Jarque and Anil K. Bera. The test statistic is always nonnegative. If it is far from zero, it signals the data do not have a normal distribution.
Color moments are measures that characterise color distribution in an image in the same way that central moments uniquely describe a probability distribution. Color moments are mainly used for color indexing purposes as features in image retrieval applications in order to compare how similar two images are based on color. Usually one image is compared to a database of digital images with pre-computed features in order to find and retrieve a similar Image. Each comparison between images results in a similarity score, and the lower this score is the more identical the two images are supposed to be.
Probability distribution fitting or simply distribution fitting is the fitting of a probability distribution to a series of data concerning the repeated measurement of a variable phenomenon.
The Cornish–Fisher expansion is an asymptotic expansion used to approximate the quantiles of a probability distribution based on its cumulants.





