Holt graph

Last updated
Holt graph
Holt graph.svg
In the Holt graph, all vertices are equivalent, and all edges are equivalent, but edges are not equivalent to their inverses.
Named afterDerek F. Holt
Vertices 27
Edges 54
Radius 3
Diameter 3
Girth 5
Automorphisms 54
Chromatic number 3
Chromatic index 5
Book thickness 3
Queue number 3
Properties Vertex-transitive
Edge-transitive
Half-transitive
Hamiltonian
Eulerian
Cayley graph
Table of graphs and parameters

In graph theory, the Holt graph or Doyle graph is the smallest half-transitive graph, that is, the smallest example of a vertex-transitive and edge-transitive graph which is not also symmetric. [1] [2] Such graphs are not common. [3] It is named after Peter G. Doyle and Derek F. Holt, who discovered the same graph independently in 1976 [4] and 1981 [5] respectively.

The Holt graph has diameter  3, radius 3 and girth  5, chromatic number  3, chromatic index  5 and is Hamiltonian with 98,472 distinct Hamiltonian cycles. [6] It is also a 4-vertex-connected and a 4-edge-connected graph. It has book thickness 3 and queue number 3. [7]

It has an automorphism group of order 54. [6] This is a smaller group than a symmetric graph with the same number of vertices and edges would have. The graph drawing on the right highlights this, in that it lacks reflectional symmetry.

The characteristic polynomial of the Holt graph is

Related Research Articles

Petersen graph Cubic graph with 10 vertices and 15 edges

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

Heawood graph

In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.

Desargues graph

In the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.

Gray graph

In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman 1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive.

Coxeter graph

In the mathematical field of graph theory, the Coxeter graph is a 3-regular graph with 28 vertices and 42 edges. It is one of the 13 known cubic distance-regular graphs. It is named after Harold Scott MacDonald Coxeter.

Pappus graph

In the mathematical field of graph theory, the Pappus graph is a bipartite 3-regular undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the cubic distance-regular graphs are known; the Pappus graph is one of the 13 such graphs.

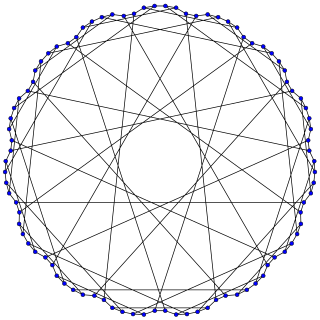
Foster graph

In the mathematical field of graph theory, the Foster graph is a bipartite 3-regular graph with 90 vertices and 135 edges.

Shrikhande graph

In the mathematical field of graph theory, the Shrikhande graph is a named graph discovered by S. S. Shrikhande in 1959. It is a strongly regular graph with 16 vertices and 48 edges, with each vertex having degree 6. Every pair of nodes has exactly two other neighbors in common, whether the pair of nodes is connected or not.

McGee graph

In the mathematical field of graph theory, the McGee graph or the (3-7)-cage is a 3-regular graph with 24 vertices and 36 edges.

Franklin graph

In the mathematical field of graph theory, the Franklin graph is a 3-regular graph with 12 vertices and 18 edges.

Folkman graph

In the mathematical field of graph theory, the Folkman graph, named after Jon Folkman, is a bipartite 4-regular graph with 20 vertices and 40 edges.

Dyck graph

In the mathematical field of graph theory, the Dyck graph is a 3-regular graph with 32 vertices and 48 edges, named after Walther von Dyck.

Nauru graph

In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.

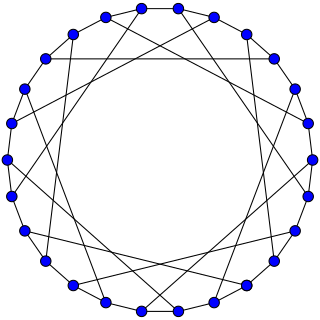
F26A graph

In the mathematical field of graph theory, the F26A graph is a symmetric bipartite cubic graph with 26 vertices and 39 edges.

Robertson graph

In the mathematical field of graph theory, the Robertson graph or (4,5)-cage, is a 4-regular undirected graph with 19 vertices and 38 edges named after Neil Robertson.

Horton graph

In the mathematical field of graph theory, the Horton graph or Horton 96-graph is a 3-regular graph with 96 vertices and 144 edges discovered by Joseph Horton. Published by Bondy and Murty in 1976, it provides a counterexample to the Tutte conjecture that every cubic 3-connected bipartite graph is Hamiltonian.

Ljubljana graph

In the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges.

Hoffman graph

In the mathematical field of graph theory, the Hoffman graph is a 4-regular graph with 16 vertices and 32 edges discovered by Alan Hoffman. Published in 1963, it is cospectral to the hypercube graph Q4.

Klein graphs

In the mathematical field of graph theory, the Klein graphs are two different but related regular graphs, each with 84 edges. Each can be embedded in the orientable surface of genus 3, in which they form dual graphs.

110-vertex Iofinova-Ivanov graph

The 110-vertex Iofinova-Ivanov graph is, in graph theory, a semi-symmetric cubic graph with 110 vertices and 165 edges.

References

  1. ↑ Doyle, P. "A 27-Vertex Graph That Is Vertex-Transitive and Edge-Transitive But Not L-Transitive." October 1998.
  2. ↑ Alspach, Brian; Marušič, Dragan; Nowitz, Lewis (1994), "Constructing Graphs which are ½-Transitive", Journal of the Australian Mathematical Society, Series A , 56 (3): 391–402, doi: 10.1017/S1446788700035564 , archived from the original on 2003-11-27.
  3. ↑ Jonathan L. Gross, Jay Yellen, Handbook of Graph Theory, CRC Press, 2004, ISBN   1-58488-090-2, p. 491.
  4. ↑ Doyle, P. G. (1976), On Transitive Graphs, Senior Thesis, Harvard College. As cited by MathWorld.
  5. ↑ Holt, Derek F. (1981), "A graph which is edge transitive but not arc transitive", Journal of Graph Theory , 5 (2): 201–204, doi:10.1002/jgt.3190050210 .
  6. 1 2 Weisstein, Eric W. "Doyle Graph". MathWorld .
  7. ↑ Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.