The Hoover index, also known as the Robin Hood index or the Schutz index, is a measure of income inequality. It is equal to the percentage of the total population's income that would have to be redistributed to make all the incomes equal.
i.e. The Hoover is the total amount (as a percentage of the national-income) by which people have less than their equal income-share.
The Hoover Index can be calculated by the following subtraction: The percentage of the people getting less than their equal-share (i.e. less than the national mean income), minus their percentage of the national income.
It can be graphically represented as the longest vertical distance between the Lorenz curve (which graphs cumulative income vs cumulative population (income-ordered population-percentile)and the 45 degree line representing perfect equality).
It would be informative to express the Hoover in terms of its average cost to individuals who get less than their equal-share:
If the Hoover is divided by the percentage of the population whose income is less than their equal-share (i.e. the mean income), that gives the average cost of that Hoover-value, per person whose income is less than their equal-share. ...that cost being expressed in terms of the national mean income.
If, instead, the Hoover is divided by the percentage of the total national income received by the people getting less than their equal-share (i.e. less than the mean income), then that gives the percentage by which those people, as a group, would get more than they currently do, if income were equal.
...in other words the cost, to them, of that Hoover value, expressed in terms of their actual current income.
That latter cost can also be gotten by dividing, instead of subtracting, the two numbers that were subtracted to get the Hoover.
...i.e. dividing the percentage of the population whose income is less than the mean by their percentage of the national income.
...and then subtracting 1.
The Hoover index is typically used in applications related to socio-economic class (SES) and health. It is conceptually one of the simplest inequality indices used in econometrics.
A more frequently encountered inequality measure is the Gini coefficient which is based on the summation, over all income-ordered population-percentiles, of the cumulative income up to each percentile. That sum is divided by the maximum value that it could have (its value with complete equality), to express it as a percentage of its maximum-possible value. The result is subtracted from one, to get a measure of inequality.
A report from the National Library of Medicine, of the National Institute of Health, described a statistical study that compared how the Robin Hood and the Gini are correlated with mortality:
Results: The Robin Hood index was positively correlated with total mortality adjusted for age (r = 0.54; P < 0.05). This association remained after adjustment for poverty (P < 0.007), where each percentage increase in the index was associated with' an increase in the total mortality of 21.68 deaths per 100,000. Effects of the index were also found for infant mortality (P = 0.013); coronary heart disease (P = 0.004); malignant neoplasms (P = 0.023); and homicide (P < 0.001). Strong associations were also found between the index and causes of death amenable to medical intervention. The Gini coefficient showed very little correlation with any of the causes of death. [1]
The Gini, like the Theil (below), is an impartial measure of inequality over the entire population. That can be of interest and use, but the Robin Hood differs, as a not-impartial examination of the total amount by which members of the population get less than their equal-share.

In economics, the Gini coefficient, also known as the Gini index or Gini ratio, is a measure of statistical dispersion intended to represent the income inequality, the wealth inequality, or the consumption inequality within a nation or a social group. It was developed by Italian statistician and sociologist Corrado Gini.

In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite set of positive real numbers by using the product of their values. The geometric mean is defined as the nth root of the product of n numbers, i.e., for a set of numbers a1, a2, ..., an, the geometric mean is defined as
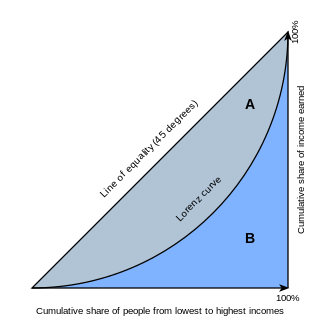
In economics, the Lorenz curve is a graphical representation of the distribution of income or of wealth. It was developed by Max O. Lorenz in 1905 for representing inequality of the wealth distribution.

The median of a set of numbers is the value separating the higher half from the lower half of a data sample, a population, or a probability distribution. For a data set, it may be thought of as the “middle" value. The basic feature of the median in describing data compared to the mean is that it is not skewed by a small proportion of extremely large or small values, and therefore provides a better representation of the center. Median income, for example, may be a better way to describe the center of the income distribution because increases in the largest incomes alone have no effect on the median. For this reason, the median is of central importance in robust statistics.
A mean is a numeric quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means in mathematics, especially in statistics. Each attempts to summarize or typify a given group of data, illustrating the magnitude and sign of the data set. Which of these measures is most illuminating depends on what is being measured, and on context and purpose.
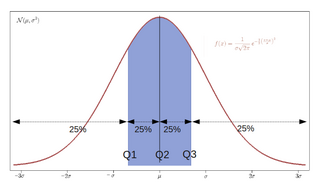
In statistics and probability, quantiles are cut points dividing the range of a probability distribution into continuous intervals with equal probabilities, or dividing the observations in a sample in the same way. There is one fewer quantile than the number of groups created. Common quantiles have special names, such as quartiles, deciles, and percentiles. The groups created are termed halves, thirds, quarters, etc., though sometimes the terms for the quantile are used for the groups created, rather than for the cut points.

In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its mean. A low standard deviation indicates that the values tend to be close to the mean of the set, while a high standard deviation indicates that the values are spread out over a wider range. The standard deviation is commonly used in the determination of what constitutes an outlier and what does not.

In welfare economics and social choice theory, a social welfare function—also called a socialordering, ranking, utility, or choicefunction—is a function that ranks a set of social states by their desirability. Each person's preferences are combined in some way to determine which outcome is considered better by society as a whole. It can be seen as mathematically formalizing Rousseau's idea of a general will.
In statistics, a k-thpercentile, also known as percentile score or centile, is a score below which a given percentage k of scores in its frequency distribution falls or a score at or below which a given percentage falls. Percentiles are expressed in the same unit of measurement as the input scores, not in percent; for example, if the scores refer to human weight, the corresponding percentiles will be expressed in kilograms or pounds. In the limit of an infinite sample size, the percentile approximates the percentile function, the inverse of the cumulative distribution function.
Income inequality metrics or income distribution metrics are used by social scientists to measure the distribution of income and economic inequality among the participants in a particular economy, such as that of a specific country or of the world in general. While different theories may try to explain how income inequality comes about, income inequality metrics simply provide a system of measurement used to determine the dispersion of incomes. The concept of inequality is distinct from poverty and fairness.
The Theil index is a statistic primarily used to measure economic inequality and other economic phenomena, though it has also been used to measure racial segregation. The Theil index TT is the same as redundancy in information theory which is the maximum possible entropy of the data minus the observed entropy. It is a special case of the generalized entropy index. It can be viewed as a measure of redundancy, lack of diversity, isolation, segregation, inequality, non-randomness, and compressibility. It was proposed by a Dutch econometrician Henri Theil (1924–2000) at the Erasmus University Rotterdam.
The Atkinson index is a measure of income inequality developed by British economist Anthony Barnes Atkinson. The measure is useful in determining which end of the distribution contributed most to the observed inequality.
The mean absolute difference (univariate) is a measure of statistical dispersion equal to the average absolute difference of two independent values drawn from a probability distribution. A related statistic is the relative mean absolute difference, which is the mean absolute difference divided by the arithmetic mean, and equal to twice the Gini coefficient. The mean absolute difference is also known as the absolute mean difference and the Gini mean difference (GMD). The mean absolute difference is sometimes denoted by Δ or as MD.

In probability and statistics, the quantile function outputs the value of a random variable such that its probability is less than or equal to an input probability value. Intuitively, the quantile function associates with a range at and below a probability input the likelihood that a random variable is realized in that range for some probability distribution. It is also called the percentile function, percent-point function, inverse cumulative distribution function or inverse distribution function.
Income segregation is the separation of various classes of people based on their income. For example, certain people cannot get into country clubs because of insufficient funds. Another example of income segregation in a neighborhood would be the schools, facilities and the characteristics of a population. Income segregation can be illustrated in countries such as the United States, where racial segregation is a major cause of income inequality.
The Lorenz asymmetry coefficient (LAC) is a summary statistic of the Lorenz curve that measures the degree of asymmetry of the curve. The Lorenz curve is used to describe the inequality in the distribution of a quantity. The most common summary statistic for the Lorenz curve is the Gini coefficient, which is an overall measure of inequality within the population. The Lorenz asymmetry coefficient can be a useful supplement to the Gini coefficient. The Lorenz asymmetry coefficient is defined as

The generalized entropy index has been proposed as a measure of income inequality in a population. It is derived from information theory as a measure of redundancy in data. In information theory a measure of redundancy can be interpreted as non-randomness or data compression; thus this interpretation also applies to this index. In addition, interpretation of biodiversity as entropy has also been proposed leading to uses of generalized entropy to quantify biodiversity.
The poverty gap index is a measure of the degree of poverty in a country. It is defined as extent to which individuals on average fall below the poverty line, and expresses it as a percentage of the poverty line.
In statistics and econometrics, the mean log deviation (MLD) is a measure of income inequality. The MLD is zero when everyone has the same income, and takes larger positive values as incomes become more unequal, especially at the high end.
The Kakwani index is a measure of the progressivity of a social intervention, and is used by social scientists, statisticians, and economists. It is named after the economist who first proposed and used it, Nanak Chand Kakwani.






















