Hurwitz quaternion

Last updated October 06, 2023

In mathematics, a Hurwitz quaternion (or Hurwitz integer) is a quaternion whose components are either all integers or all half-integers (halves of odd integers; a mixture of integers and half-integers is excluded). The set of all Hurwitz quaternions is

Structure of the ring of Hurwitz quaternions

As an additive group, H is free abelian with generators {(1 + i + j + k) / 2, i, j, k}. It therefore forms a lattice in R⁴. This lattice is known as the F₄ lattice since it is the root lattice of the semisimple Lie algebra F₄. The Lipschitz quaternions L form an index 2 sublattice of H.

The group of units in L is the order 8 quaternion group Q = {±1, ±i, ±j, ±k}. The group of units in H is a nonabelian group of order 24 known as the binary tetrahedral group. The elements of this group include the 8 elements of Q along with the 16 quaternions {(±1 ± i ± j ± k) / 2}, where signs may be taken in any combination. The quaternion group is a normal subgroup of the binary tetrahedral group U(H). The elements of U(H), which all have norm 1, form the vertices of the 24-cell inscribed in the 3-sphere.

The Hurwitz quaternions form an order (in the sense of ring theory) in the division ring of quaternions with rational components. It is in fact a maximal order; this accounts for its importance. The Lipschitz quaternions, which are the more obvious candidate for the idea of an integral quaternion, also form an order. However, this latter order is not a maximal one, and therefore (as it turns out) less suitable for developing a theory of left ideals comparable to that of algebraic number theory. What Adolf Hurwitz realised, therefore, was that this definition of Hurwitz integral quaternion is the better one to operate with. For a non-commutative ring such as H, maximal orders need not be unique, so one needs to fix a maximal order, in carrying over the concept of an algebraic integer.

The lattice of Hurwitz quaternions

The (arithmetic, or field) norm of a Hurwitz quaternion a + bi + cj + dk, given by a² + b² + c² + d², is always an integer. By a theorem of Lagrange every nonnegative integer can be written as a sum of at most four squares. Thus, every nonnegative integer is the norm of some Lipschitz (or Hurwitz) quaternion. More precisely, the number c(n) of Hurwitz quaternions of given positive norm n is 24 times the sum of the odd divisors of n. The generating function of the numbers c(n) is given by the level 2 weight 2 modular form

2E_{2}(2\tau )-E_{2}(\tau )=\sum _{n}c(n)q^{n}=1+24q+24q^{2}+96q^{3}+24q^{4}+144q^{5}+\dots

OEIS: A004011

where

q=e^{2\pi i\tau }

and

E_{2}(\tau )=1-24\sum _{n}\sigma _{1}(n)q^{n}

is the weight 2 level 1 Eisenstein series (which is a quasimodular form) and σ₁(n) is the sum of the divisors of n.

Factorization into irreducible elements

A Hurwitz integer is called irreducible if it is not 0 or a unit and is not a product of non-units. A Hurwitz integer is irreducible if and only if its norm is a prime number. The irreducible quaternions are sometimes called prime quaternions, but this can be misleading as they are not primes in the usual sense of commutative algebra: it is possible for an irreducible quaternion to divide a product ab without dividing either a or b. Every Hurwitz quaternion can be factored as a product of irreducible quaternions. This factorization is not in general unique, even up to units and order, because a positive odd prime p can be written in 24(p+1) ways as a product of two irreducible Hurwitz quaternions of norm p, and for large p these cannot all be equivalent under left and right multiplication by units as there are only 24 units. However, if one excludes this case then there is a version of unique factorization. More precisely, every Hurwitz quaternion can be written uniquely as the product of a positive integer and a primitive quaternion (a Hurwitz quaternion not divisible by any integer greater than 1). The factorization of a primitive quaternion into irreducibles is unique up to order and units in the following sense: if

p₀p₁...p_n

and

q₀q₁...q_n

are two factorizations of some primitive Hurwitz quaternion into irreducible quaternions where p_k has the same norm as q_k for all k, then

{\begin{aligned}q_{0}&=p_{0}u_{1}\\q_{1}&=u_{1}^{-1}p_{1}u_{2}\\&\,\,\,\vdots \\q_{n}&=u_{n}^{-1}p_{n}\end{aligned}}

for some units u_k.

Division with remainder

The ordinary integers and the Gaussian integers allow a division with remainder or Euclidean division.

For positive integers N and D, there is always a quotient Q and a nonnegative remainder R such that

N = QD + R where R < D.

For complex or Gaussian integers N = a + ib and D = c + id, with the norm N(D) > 0, there always exist Q = p + iq and R = r + is such that

N = QD + R, where N(R) < N(D).

However, for Lipschitz integers N = (a, b, c, d) and D = (e, f, g, h) it can happen that N(R) = N(D). This motivated a switch to Hurwitz integers, for which the condition N(R) < N(D) is guaranteed.^[1]

Many algorithms depend on division with remainder, for example, Euclid's algorithm for the greatest common divisor.

Related Research Articles

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements . It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

In mathematics, specifically abstract algebra, an integral domain is a nonzero commutative ring in which the product of any two nonzero elements is nonzero. Integral domains are generalizations of the ring of integers and provide a natural setting for studying divisibility. In an integral domain, every nonzero element a has the cancellation property, that is, if a ≠ 0, an equality ab = ac implies b = c.

In number theory, a Gaussian integer is a complex number whose real and imaginary parts are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as $or$

In mathematics, the octonions are a normed division algebra over the real numbers, a kind of hypercomplex number system. The octonions are usually represented by the capital letter O, using boldface $O$ or blackboard bold $. Octonions have eight dimensions; twice the number of dimensions of the quaternions, of which they are an extension. They are noncommutative and nonassociative, but satisfy a weaker form of associativity; namely, they are alternative. They are also power associative.$

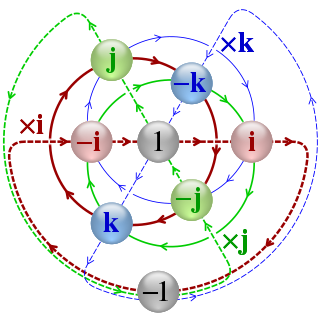
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space, or, equivalently, as the quotient of two vectors. Multiplication of quaternions is noncommutative.

In mathematics, a unique factorization domain (UFD) is a ring in which a statement analogous to the fundamental theorem of arithmetic holds. Specifically, a UFD is an integral domain in which every non-zero non-unit element can be written as a product of irreducible elements, uniquely up to order and units.

Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic objects such as algebraic number fields and their rings of integers, finite fields, and function fields. These properties, such as whether a ring admits unique factorization, the behavior of ideals, and the Galois groups of fields, can resolve questions of primary importance in number theory, like the existence of solutions to Diophantine equations.

In mathematics, an irreducible polynomial is, roughly speaking, a polynomial that cannot be factored into the product of two non-constant polynomials. The property of irreducibility depends on the nature of the coefficients that are accepted for the possible factors, that is, the field to which the coefficients of the polynomial and its possible factors are supposed to belong. For example, the polynomial $x 2 - 2$ is a polynomial with integer coefficients, but, as every integer is also a real number, it is also a polynomial with real coefficients. It is irreducible if it is considered as a polynomial with integer coefficients, but it factors as $if it is considered as a polynomial with real coefficients. One says that the polynomial x 2 - 2 is irreducible over the integers but not over the reals.$

Lagrange's four-square theorem, also known as Bachet's conjecture, states that every natural number can be represented as a sum of four non-negative integer squares. That is, the squares form an additive basis of order four.

In mathematics, the ring of integers of an algebraic number field $is the ring of all algebraic integers contained in . An algebraic integer is a root of a monic polynomial with integer coefficients: . This ring is often denoted by or . Since any integer belongs to and is an integral element of, the ring is always a subring of .$

In mathematics, an arithmetic group is a group obtained as the integer points of an algebraic group, for example $They arise naturally in the study of arithmetic properties of quadratic forms and other classical topics in number theory. They also give rise to very interesting examples of Riemannian manifolds and hence are objects of interest in differential geometry and topology. Finally, these two topics join in the theory of automorphic forms which is fundamental in modern number theory.$

In mathematics, an order in the sense of ring theory is a subring $of a ring, such that$

is a finite-dimensional algebra over the field $of rational numbers$
$spans over, and$
$is a -lattice in .$

In mathematics, the E₈ lattice is a special lattice in R⁸. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8. The name derives from the fact that it is the root lattice of the E₈ root system.

In mathematics, the Eisenstein integers, occasionally also known as Eulerian integers, are the complex numbers of the form

In mathematics and computer algebra, factorization of polynomials or polynomial factorization expresses a polynomial with coefficients in a given field or in the integers as the product of irreducible factors with coefficients in the same domain. Polynomial factorization is one of the fundamental components of computer algebra systems.

In the mathematical theory of Riemann surfaces, the first Hurwitz triplet is a triple of distinct Hurwitz surfaces with the identical automorphism group of the lowest possible genus, namely 14. The explanation for this phenomenon is arithmetic. Namely, in the ring of integers of the appropriate number field, the rational prime 13 splits as a product of three distinct prime ideals. The principal congruence subgroups defined by the triplet of primes produce Fuchsian groups corresponding to the triplet of Riemann surfaces.

The Hurwitz quaternion order is a specific order in a quaternion algebra over a suitable number field. The order is of particular importance in Riemann surface theory, in connection with surfaces with maximal symmetry, namely the Hurwitz surfaces. The Hurwitz quaternion order was studied in 1967 by Goro Shimura, but first explicitly described by Noam Elkies in 1998. For an alternative use of the term, see Hurwitz quaternion.

In number theory, quadratic integers are a generalization of the usual integers to quadratic fields. Quadratic integers are algebraic integers of degree two, that is, solutions of equations of the form

In the area of modern algebra known as group theory, the Conway group is a sporadic simple group of order

Arithmetic Fuchsian groups are a special class of Fuchsian groups constructed using orders in quaternion algebras. They are particular instances of arithmetic groups. The prototypical example of an arithmetic Fuchsian group is the modular group $. They, and the hyperbolic surface associated to their action on the hyperbolic plane often exhibit particularly regular behaviour among Fuchsian groups and hyperbolic surfaces.$

References

↑ Conway & Smith 2003 , p. 56

Conway, John Horton; Smith, Derek A. (2003). On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry. A.K. Peters. ISBN 1-56881-134-9.
Hurwitz, Adolf (2013) [1919]. Vorlesungen Über die Zahlentheorie der Quaternionen. Springer-Verlag. ISBN 978-3-642-47536-8. JFM 47.0106.01.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Conway & Smith 2003 , p. 56

[1]