
Jack Joseph Dongarra is an American computer scientist and mathematician. He is a University Distinguished Professor of Computer Science in the Electrical Engineering and Computer Science Department at the University of Tennessee. He holds the position of a Distinguished Research Staff member in the Computer Science and Mathematics Division at Oak Ridge National Laboratory, Turing Fellowship in the School of Mathematics at the University of Manchester, and is an adjunct professor and teacher in the Computer Science Department at Rice University. He served as a faculty fellow at the Texas A&M University Institute for Advanced Study (2014–2018). Dongarra is the founding director of the Innovative Computing Laboratory at the University of Tennessee. He was the recipient of the Turing Award in 2021.
In numerical analysis, a multigrid method is an algorithm for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior. For example, many basic relaxation methods exhibit different rates of convergence for short- and long-wavelength components, suggesting these different scales be treated differently, as in a Fourier analysis approach to multigrid. MG methods can be used as solvers as well as preconditioners.
The Portable, Extensible Toolkit for Scientific Computation, is a suite of data structures and routines developed by Argonne National Laboratory for the scalable (parallel) solution of scientific applications modeled by partial differential equations. It employs the Message Passing Interface (MPI) standard for all message-passing communication. PETSc is the world’s most widely used parallel numerical software library for partial differential equations and sparse matrix computations. PETSc received an R&D 100 Award in 2009. The PETSc Core Development Group won the SIAM/ACM Prize in Computational Science and Engineering for 2015.
In mathematics, in particular numerical analysis, the FETI method is an iterative substructuring method for solving systems of linear equations from the finite element method for the solution of elliptic partial differential equations, in particular in computational mechanics In each iteration, FETI requires the solution of a Neumann problem in each substructure and the solution of a coarse problem. The simplest version of FETI with no preconditioner in the substructure is scalable with the number of substructures but the condition number grows polynomially with the number of elements per substructure. FETI with a preconditioner consisting of the solution of a Dirichlet problem in each substructure is scalable with the number of substructures and its condition number grows only polylogarithmically with the number of elements per substructure. The coarse space in FETI consists of the nullspace on each substructure.

Lis is a scalable parallel software library to solve discretized linear equations and eigenvalue problems that mainly arise from the numerical solution of partial differential equations using iterative methods. Although it is designed for parallel computers, the library can be used without being conscious of parallel processing.
In numerical analysis, BDDC (balancing domain decomposition by constraints) is a domain decomposition method for solving large symmetric, positive definite systems of linear equations that arise from the finite element method. BDDC is used as a preconditioner to the conjugate gradient method. A specific version of BDDC is characterized by the choice of coarse degrees of freedom, which can be values at the corners of the subdomains, or averages over the edges or the faces of the interface between the subdomains. One application of the BDDC preconditioner then combines the solution of local problems on each subdomains with the solution of a global coarse problem with the coarse degrees of freedom as the unknowns. The local problems on different subdomains are completely independent of each other, so the method is suitable for parallel computing. With a proper choice of the coarse degrees of freedom (corners in 2D, corners plus edges or corners plus faces in 3D) and with regular subdomain shapes, the condition number of the method is bounded when increasing the number of subdomains, and it grows only very slowly with the number of elements per subdomain. Thus the number of iterations is bounded in the same way, and the method scales well with the problem size and the number of subdomains.
The FETI-DP method is a domain decomposition method that enforces equality of the solution at subdomain interfaces by Lagrange multipliers except at subdomain corners, which remain primal variables. The first mathematical analysis of the method was provided by Mandel and Tezaur. The method was further improved by enforcing the equality of averages across the edges or faces on subdomain interfaces which is important for parallel scalability for 3D problems. FETI-DP is a simplification and a better performing version of FETI. The eigenvalues of FETI-DP are same as those of BDDC, except for the eigenvalue equal to one, and so the performance of FETI-DP and BDDC is essentially same.
In numerical analysis, the balancing domain decomposition method (BDD) is an iterative method to find the solution of a symmetric positive definite system of linear algebraic equations arising from the finite element method. In each iteration, it combines the solution of local problems on non-overlapping subdomains with a coarse problem created from the subdomain nullspaces. BDD requires only solution of subdomain problems rather than access to the matrices of those problems, so it is applicable to situations where only the solution operators are available, such as in oil reservoir simulation by mixed finite elements. In its original formulation, BDD performs well only for 2nd order problems, such elasticity in 2D and 3D. For 4th order problems, such as plate bending, it needs to be modified by adding to the coarse problem special basis functions that enforce continuity of the solution at subdomain corners, which makes it however more expensive. The BDDC method uses the same corner basis functions as, but in an additive rather than multiplicative fashion. The dual counterpart to BDD is FETI, which enforces the equality of the solution between the subdomain by Lagrange multipliers. The base versions of BDD and FETI are not mathematically equivalent, though a special version of FETI designed to be robust for hard problems has the same eigenvalues and thus essentially the same performance as BDD.
In numerical analysis, the Schur complement method, named after Issai Schur, is the basic and the earliest version of non-overlapping domain decomposition method, also called iterative substructuring. A finite element problem is split into non-overlapping subdomains, and the unknowns in the interiors of the subdomains are eliminated. The remaining Schur complement system on the unknowns associated with subdomain interfaces is solved by the conjugate gradient method.

The FEniCS Project is a collection of free and open-source software components with the common goal to enable automated solution of differential equations. The components provide scientific computing tools for working with computational meshes, finite-element variational formulations of ordinary and partial differential equations, and numerical linear algebra.
OOFEM is a free and open-source multi-physics finite element code with object oriented architecture. The aim of this project is to provide efficient and robust tool for FEM computations as well as to offer highly modular and extensible environment for development.
ARPACK, the ARnoldi PACKage, is a numerical software library written in FORTRAN 77 for solving large scale eigenvalue problems in the matrix-free fashion.
Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) is a matrix-free method for finding the largest eigenvalues and the corresponding eigenvectors of a symmetric generalized eigenvalue problem
SLEPc is a software library for the parallel computation of eigenvalues and eigenvectors of large, sparse matrices. It can be seen as a module of PETSc that provides solvers for different types of eigenproblems, including linear and nonlinear, as well as the SVD. Recent versions also include support for matrix functions. It uses the MPI standard for parallelization. Both real and complex arithmetic are supported, with single, double and quadruple precision.

SU2 is a suite of open-source software tools written in C++ for the numerical solution of partial differential equations (PDE) and performing PDE-constrained optimization. The primary applications are computational fluid dynamics and aerodynamic shape optimization, but has been extended to treat more general equations such as electrodynamics and chemically reacting flows. SU2 supports continuous and discrete adjoint for calculating the sensitivities/gradients of a scalar field.
MoFEM is an open source finite element analysis code developed and maintained at the University of Glasgow. MoFEM is tailored for the solution of multi-physics problems with arbitrary levels of approximation, different levels of mesh refinement and optimised for high-performance computing. MoFEM is the blend of the Boost MultiIndex containers, MOAB and PETSc. MoFEM is developed in C++ and it is open-source software under the GNU Lesser General Public License (GPL).
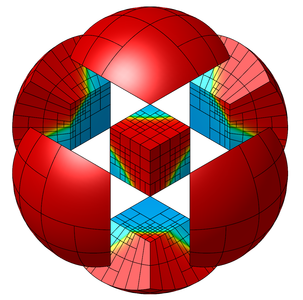
MFEM is an open-source C++ library for solving partial differential equations using the finite element method, developed and maintained by researchers at the Lawrence Livermore National Laboratory and the MFEM open-source community on GitHub. MFEM is free software released under a BSD license.
Ulrike Meier Yang is a German-American applied mathematician and computer scientist specializing in numerical algorithms for scientific computing. She directs the Mathematical Algorithms & Computing group in the Center for Applied Scientific Computing at the Lawrence Livermore National Laboratory, and is one of the developers of the Hypre library of parallel methods for solving linear systems.




