Implicit data structure

Last updated February 06, 2024

In computer science, an implicit data structure or space-efficient data structure is a data structure that stores very little information other than the main or required data: a data structure that requires low overhead. They are called "implicit" because the position of the elements carries meaning and relationship between elements; this is contrasted with the use of pointers to give an explicit relationship between elements. Definitions of "low overhead" vary, but generally means constant overhead; in big O notation, O(1) overhead. A less restrictive definition is a succinct data structure, which allows greater overhead.

Definition

An implicit data structure is one with constant $O (1)$ space overhead (above the information-theoretic lower bound).

Historically, Munro & Suwanda (1980) defined an implicit data structure (and algorithms acting on one) as one "in which structural information is implicit in the way data are stored, rather than explicit in pointers." They are somewhat vague in the definition, defining it most strictly as a single array, with only the size retained (a single number of overhead),^[1] or more loosely as a data structure with constant overhead ( $O (1)$ ).^[2] This latter definition is today more standard, and the still-looser notion of a data structure with non-constant but small $o (n)$ overhead is today known as a succinct data structure, as defined by Jacobson (1988); it was referred to as semi-implicit by Munro & Suwanda (1980).^[3]

A fundamental distinction is between static data structures (read-only) and dynamic data structures (which can be modified). Simple implicit data structures, such as representing a sorted list as an array, may be very efficient as a static data structure, but inefficient as a dynamic data structure, due to modification operations (such as insertion in the case of a sorted list) being inefficient.

Examples

A trivial example of an implicit data structure is an array data structure , which is an implicit data structure for a list, and requires only the constant overhead of the length; unlike a linked list, which has a pointer associated with each data element, which explicitly gives the relationship from one element to the next. Similarly, a null-terminated string is an implicit data structure for a string (list of characters). These are considered very simple because they are static data structures (read-only), and only admit the simple operation of iteration over the elements.

Similarly simple is representing a multi-dimensional array as a single 1-dimensional array, together with its dimensions. For example, representing an m × n array as a single list of length m·n, together with the numbers m and n (instead of as a 1-dimensional array of pointers to each 1-dimensional subarray). The elements need not be of the same type, and a table of data (a list of records) may similarly be represented implicitly as a flat (1-dimensional) list, together with the length of each field, so long as each field has uniform size (so a single size can be used per field, not per record).

A less trivial example is representing a sorted list by a sorted array , which allows search in logarithmic time by binary search. Contrast with a search tree, specifically a binary search tree, which also allows logarithmic-time search, but requires pointers. A sorted array is only efficient as a static data structure, as modifying the list is slow – unlike a binary search tree – but does not require the space overhead of a tree.

An important example of an implicit data structure is representing a perfect binary tree as a list, in increasing order of depth, so root, first left child, first right child, first left child of first left child, etc. Such a tree occurs notably for an ancestry chart to a given depth, and the implicit representation is known as an Ahnentafel (ancestor table).

This can be generalized to a complete binary tree (where the last level may be incomplete), which yields the best-known example of an implicit data structure, namely the binary heap , which is an implicit data structure for a priority queue. This is more sophisticated than earlier examples because it allows multiple operations, and is an efficient dynamic data structure (it allows efficient modification of the data): not only top, but also insert and pop.

More sophisticated implicit data structures include the beap (bi-parental heap).

History

The trivial examples of lists or tables of values date to prehistory, while historically non-trivial implicit data structures date at least to the Ahnentafel, which was introduced by Michaël Eytzinger in 1590 for use in genealogy. In formal computer science, the first implicit data structure is generally considered to be the sorted list, used for binary search, which was introduced by John Mauchly in 1946, in the Moore School Lectures, the first ever set of lectures regarding any computer-related topic.^[4]^[5] The binary heap was introduced in Williams (1964) to implement the heapsort.^[5] The notion of an implicit data structure was formalized in Munro & Suwanda (1980), as part of introducing and analyzing the beap.^[5]

Related Research Articles

In computer science, an array is a data structure consisting of a collection of elements, of same memory size, each identified by at least one array index or key. An array is stored such that the position of each element can be computed from its index tuple by a mathematical formula. The simplest type of data structure is a linear array, also called one-dimensional array.

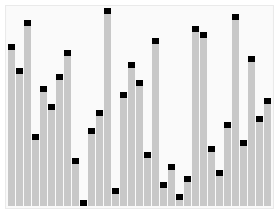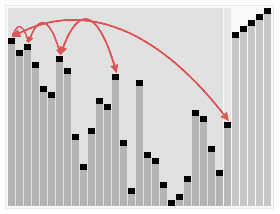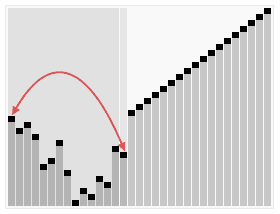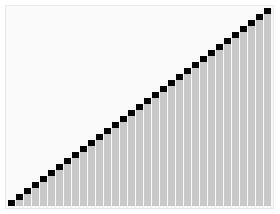
<span class="mw-page-title-main">Heapsort</span> A sorting algorithm which uses the heap data structure

In computer science, heapsort is a comparison-based sorting algorithm which can be thought of as "an implementation of selection sort using the right data structure." Like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to efficiently find the largest element in each step.

<span class="mw-page-title-main">Heap (data structure)</span> Computer science data structure

In computer science, a heap is a tree-based data structure that satisfies the heap property: In a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.

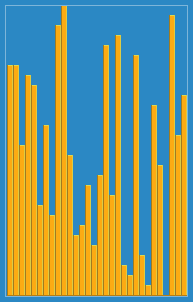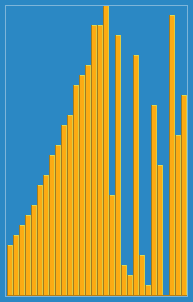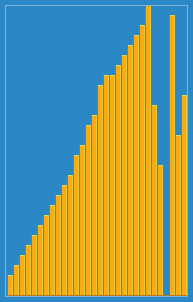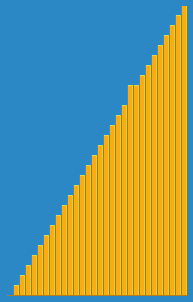
<span class="mw-page-title-main">Insertion sort</span> Sorting algorithm

Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:

In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes which together represent a sequence. In its most basic form, each node contains data, and a reference to the next node in the sequence. This structure allows for efficient insertion or removal of elements from any position in the sequence during iteration. More complex variants add additional links, allowing more efficient insertion or removal of nodes at arbitrary positions. A drawback of linked lists is that data access time is linear in respect to the number of nodes in the list. Because nodes are serially linked, accessing any node requires that the prior node be accessed beforehand. Faster access, such as random access, is not feasible. Arrays have better cache locality compared to linked lists.

<span class="mw-page-title-main">Sorting algorithm</span> Algorithm that arranges lists in order

In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output.

<span class="mw-page-title-main">Binary heap</span> Variant of heap data structure

A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues. The binary heap was introduced by J. W. J. Williams in 1964, as a data structure for heapsort.

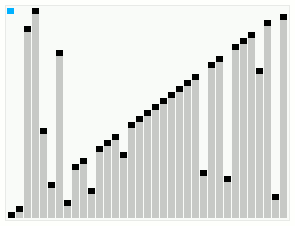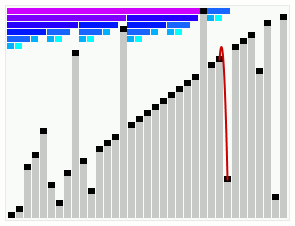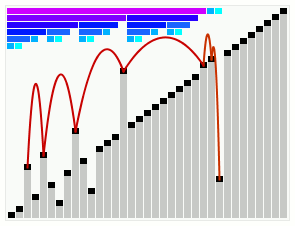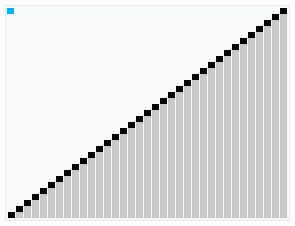
<span class="mw-page-title-main">Smoothsort</span> Comparison-based sorting algorithm

In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981. Like heapsort, smoothsort is an in-place algorithm with an upper bound of $O (n log n)$ operations (see big O notation), but it is not a stable sort. The advantage of smoothsort is that it comes closer to $O (n)$ time if the input is already sorted to some degree, whereas heapsort averages $O (n log n)$ regardless of the initial sorted state.

In computer science, a self-balancing binary search tree (BST) is any node-based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions. These operations when designed for a self-balancing binary search tree, contain precautionary measures against boundlessly increasing tree height, so that these abstract data structures receive the attribute "self-balancing".

In mathematical analysis and computer science, functions which are Z-order, Lebesgue curve, Morton space-filling curve, Morton order or Morton code map multidimensional data to one dimension while preserving locality of the data points. It is named in France after Henri Lebesgue, who studied it in 1904, and named in the United States after Guy Macdonald Morton, who first applied the order to file sequencing in 1966. The z-value of a point in multidimensions is simply calculated by interleaving the binary representations of its coordinate values. Once the data are sorted into this ordering, any one-dimensional data structure can be used, such as simple one dimensional arrays, binary search trees, B-trees, skip lists or hash tables. The resulting ordering can equivalently be described as the order one would get from a depth-first traversal of a quadtree or octree.

<span class="mw-page-title-main">Quicksort</span> Divide and conquer sorting algorithm

Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961. It is still a commonly used algorithm for sorting. Overall, it is slightly faster than merge sort and heapsort for randomized data, particularly on larger distributions.

In computer science, an algorithm is said to be asymptotically optimal if, roughly speaking, for large inputs it performs at worst a constant factor worse than the best possible algorithm. It is a term commonly encountered in computer science research as a result of widespread use of big-O notation.

<span class="mw-page-title-main">Beap</span> Data structure

A beap, or bi-parental heap, is a data structure for a set that enables elements to be located, inserted, or deleted in sublinear time. In a beap, each element is stored in a node with up to two parents and up to two children, with the property that the value of a parent node is never greater than the value of either of its children.

<span class="mw-page-title-main">Recursion (computer science)</span> Use of functions that call themselves

In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.

The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.

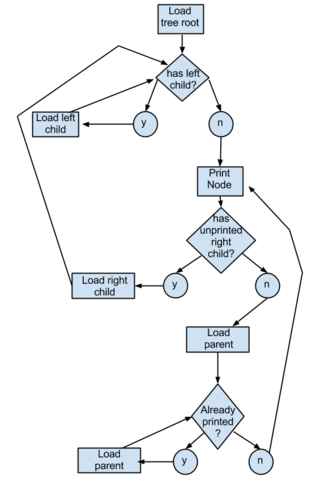
A tree sort is a sort algorithm that builds a binary search tree from the elements to be sorted, and then traverses the tree (in-order) so that the elements come out in sorted order. Its typical use is sorting elements online: after each insertion, the set of elements seen so far is available in sorted order.

In computer science, a succinct data structure is a data structure which uses an amount of space that is "close" to the information-theoretic lower bound, but still allows for efficient query operations. The concept was originally introduced by Jacobson to encode bit vectors, (unlabeled) trees, and planar graphs. Unlike general lossless data compression algorithms, succinct data structures retain the ability to use them in-place, without decompressing them first. A related notion is that of a compressed data structure, insofar as the size of the stored or encoded data similarly depends upon the specific content of the data itself.

In computer science, a search data structure is any data structure that allows the efficient retrieval of specific items from a set of items, such as a specific record from a database.

In computer science, input enhancement is the principle that processing a given input to a problem and altering it in a specific way will increase runtime efficiency or space efficiency, or both. The altered input is usually stored and accessed to simplify the problem. By exploiting the structure and properties of the inputs, input enhancement creates various speed-ups in the efficiency of the algorithm.

In computer science, a weak heap is a data structure for priority queues, combining features of the binary heap and binomial heap. It can be stored in an array as an implicit binary tree like a binary heap, and has the efficiency guarantees of binomial heaps.

References

↑ "Thus, only a simple array is needed for the data.", p. 236; "We will draw no formal distinction between a pointer and an integer (index) in the range $[0,N]$ . A data structure is then implicit, if the only such integer which need be retained is N itself.", p. 238
↑ "... one might prefer to permit a constant number of pointers to be retained and still designate the structure as implicit.", p. 238
↑ "We will also suggest two structures which might be described as “semi-implicit,” in that a variable, but o(N), number of pointers (indices) is kept.", p. 238
↑ Knuth 1998, §6.2.1 ("Searching an ordered table"), subsection "History and bibliography".
1 2 3 Franceschini, Gianni; Munro, J. Ian (2006). Implicit dictionaries with O(1) modifications per update and fast search. Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithms. Miami, FL, United States. pp. 404–413. doi:10.1145/1109557.1109603.

Jacobson, G. J (1988). Succinct static data structures (Ph.D.). Pittsburgh, PA: Carnegie Mellon University.
Knuth, Donald (1998). Sorting and searching. The Art of Computer Programming. Vol. 3 (2nd ed.). Reading, MA: Addison-Wesley Professional. ISBN 978-0-201-89685-5.
Munro, J.Ian; Suwanda, Hendra (October 1980). "Implicit data structures for fast search and update". Journal of Computer and System Sciences . 21 (2): 236–250. doi: 10.1016/0022-0000(80)90037-9 .
Williams, J. W. J. (June 1964). "Algorithm 232 - Heapsort". Communications of the ACM. 7 (6): 347–348. doi:10.1145/512274.512284.