Related Research Articles

The travelling salesman problem asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.

In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.

Linear programming (LP), also called linear optimization, is a method to achieve the best outcome in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming.

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
In geometry, a geodesic is a curve representing in some sense the shortest path (arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line".
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, source reconstruction in acoustics, or calculating the density of the Earth from measurements of its gravity field. It is called an inverse problem because it starts with the effects and then calculates the causes. It is the inverse of a forward problem, which starts with the causes and then calculates the effects.

Optimal control theory is a branch of mathematical optimization that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized. It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the moon with minimum fuel expenditure. Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy. A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory.
Stress–strain analysis is an engineering discipline that uses many methods to determine the stresses and strains in materials and structures subjected to forces. In continuum mechanics, stress is a physical quantity that expresses the internal forces that neighboring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material.
Topology optimization (TO) is a mathematical method that optimizes material layout within a given design space, for a given set of loads, boundary conditions and constraints with the goal of maximizing the performance of the system. Topology optimization is different from shape optimization and sizing optimization in the sense that the design can attain any shape within the design space, instead of dealing with predefined configurations.
In mathematics, computer science and economics, an optimization problem is the problem of finding the best solution from all feasible solutions.
Shape optimization is part of the field of optimal control theory. The typical problem is to find the shape which is optimal in that it minimizes a certain cost functional while satisfying given constraints. In many cases, the functional being solved depends on the solution of a given partial differential equation defined on the variable domain.
Trajectory optimization is the process of designing a trajectory that minimizes some measure of performance while satisfying a set of constraints. Generally speaking, trajectory optimization is a technique for computing an open-loop solution to an optimal control problem. It is often used for systems where computing the full closed-loop solution is not required, impractical or impossible. If a trajectory optimization problem can be solved at a rate given by the inverse of the Lipschitz constant, then it can be used iteratively to generate a closed-loop solution in the sense of Caratheodory. If only the first step of the trajectory is executed for an infinite-horizon problem, then this is known as Model Predictive Control (MPC).

In mathematics, a space is a set with some added structure. While modern mathematics uses many types of spaces, such as Euclidean spaces, linear spaces, topological spaces, Hilbert spaces, or probability spaces, it does not define the notion of "space" itself.
Nearest neighbor search (NNS), as a form of proximity search, is the optimization problem of finding the point in a given set that is closest to a given point. Closeness is typically expressed in terms of a dissimilarity function: the less similar the objects, the larger the function values.
In the field of calculus of variations in mathematics, the method of Lagrange multipliers on Banach spaces can be used to solve certain infinite-dimensional constrained optimization problems. The method is a generalization of the classical method of Lagrange multipliers as used to find extrema of a function of finitely many variables.
In optimization theory, semi-infinite programming (SIP) is an optimization problem with a finite number of variables and an infinite number of constraints, or an infinite number of variables and a finite number of constraints. In the former case the constraints are typically parameterized.
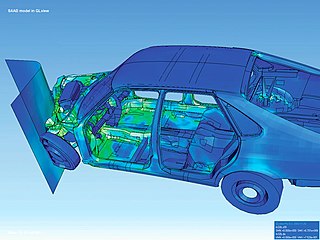
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential.
References
- David Luenberger (1997). Optimization by Vector Space Methods. John Wiley & Sons. ISBN 0-471-18117-X.
- Edward J. Anderson and Peter Nash, Linear Programming in Infinite-Dimensional Spaces, Wiley, 1987.
- M. A. Goberna and M. A. López, Linear Semi-Infinite Optimization, Wiley, 1998.
- Cassel, Kevin W.: Variational Methods with Applications in Science and Engineering, Cambridge University Press, 2013.