Jarkko J. Kari is a Finnish mathematician and computer scientist, known for his contributions to the theory of Wang tiles and cellular automata. Kari is currently a professor at the Department of Mathematics, University of Turku. [1]
Jarkko J. Kari is a Finnish mathematician and computer scientist, known for his contributions to the theory of Wang tiles and cellular automata. Kari is currently a professor at the Department of Mathematics, University of Turku. [1]
Kari received his Ph.D. in 1990 from the University of Turku; his dissertation, supervised by Arto Salomaa. [2]
He married Lila Kari, a later mathematics student at Turku; they divorced, and afterwards Lila Kari became a professor of computer science at the University of Western Ontario in Canada. [3]
Wang tiles are unit squares with colored markings on each side; they may be used to tesselate the plane, but only with tiles that have matching colors on adjoining edges. The problem of determining whether a set of Wang tiles forms a valid tessellation is undecidable, and its undecidability rests on finding sets of Wang tiles that can only tesselate the plane aperiodically, in such a way that no translation of the plane is a symmetry of the tiling. The first set of aperiodic Wang tiles found, by Robert Berger, had over 20,000 different tiles in it. Kari reduced the size of this set to only 14, by finding a set of tiles that (when used to tile the plane) simulates the construction of a Beatty sequence by Mealy machines. [4] The same approach was later shown to lead to aperiodic sets of 13 tiles, the minimum known. [5] Kari has also shown that the Wang tiling problem remains undecidable in the hyperbolic plane, [6] and has discovered sets of Wang tiles with additional mathematical properties. [7]
Kari has also used the Wang tiling problem as the basis of proofs that several algorithmic problems in the theory of cellular automata are undecidable. In particular, in his thesis research, he showed that it is undecidable to determine whether a given cellular automaton rule in two or more dimensions is reversible. [8] For one-dimensional cellular automata, reversibility is known to be decidable, and Kari has provided tight bounds on the size of the neighborhood needed to simulate the reverse dynamics of reversible one-dimensional automata. [9]
A cellular automaton is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling.
Wang tiles, first proposed by mathematician, logician, and philosopher Hao Wang in 1961, is a class of formal systems. They are modeled visually by square tiles with a color on each side. A set of such tiles is selected, and copies of the tiles are arranged side by side with matching colors, without rotating or reflecting them.
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.
An aperiodic tiling is a non-periodic tiling with the additional property that it does not contain arbitrarily large periodic regions or patches. A set of tile-types is aperiodic if copies of these tiles can form only non-periodic tilings.
In a cellular automaton, a Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way. John Tukey named these configurations after the Garden of Eden in Abrahamic religions, which was created out of nowhere.
A block cellular automaton or partitioning cellular automaton is a special kind of cellular automaton in which the lattice of cells is divided into non-overlapping blocks and the transition rule is applied to a whole block at a time rather than a single cell. Block cellular automata are useful for simulations of physical quantities, because it is straightforward to choose transition rules that obey physical constraints such as reversibility and conservation laws.
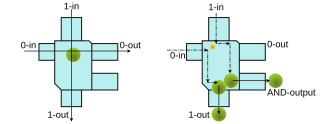
A billiard-ball computer, a type of conservative logic circuit, is an idealized model of a reversible mechanical computer based on Newtonian dynamics, proposed in 1982 by Edward Fredkin and Tommaso Toffoli. Instead of using electronic signals like a conventional computer, it relies on the motion of spherical billiard balls in a friction-free environment made of buffers against which the balls bounce perfectly. It was devised to investigate the relation between computation and reversible processes in physics.
A quantum cellular automaton (QCA) is an abstract model of quantum computation, devised in analogy to conventional models of cellular automata introduced by John von Neumann. The same name may also refer to quantum dot cellular automata, which are a proposed physical implementation of "classical" cellular automata by exploiting quantum mechanical phenomena. QCA have attracted a lot of attention as a result of its extremely small feature size and its ultra-low power consumption, making it one candidate for replacing CMOS technology.
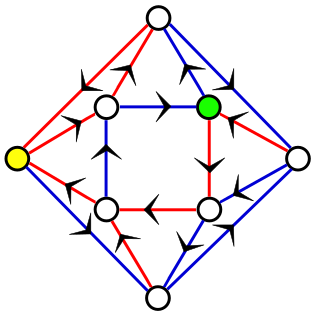
In computer science, more precisely, in the theory of deterministic finite automata (DFA), a synchronizing word or reset sequence is a word in the input alphabet of the DFA that sends any state of the DFA to one and the same state. That is, if an ensemble of copies of the DFA are each started in different states, and all of the copies process the synchronizing word, they will all end up in the same state. Not every DFA has a synchronizing word; for instance, a DFA with two states, one for words of even length and one for words of odd length, can never be synchronized.
The Curtis–Hedlund–Lyndon theorem is a mathematical characterization of cellular automata in terms of their symbolic dynamics. It is named after Morton L. Curtis, Gustav A. Hedlund, and Roger Lyndon; in his 1969 paper stating the theorem, Hedlund credited Curtis and Lyndon as co-discoverers. It has been called "one of the fundamental results in symbolic dynamics".
In graph theory the road coloring theorem, known previously as the road coloring conjecture, deals with synchronized instructions. The issue involves whether by using such instructions, one can reach or locate an object or destination from any other point within a network. In the real world, this phenomenon would be as if you called a friend to ask for directions to his house, and he gave you a set of directions that worked no matter where you started from. This theorem also has implications in symbolic dynamics.
A Penrose tiling is an example of an aperiodic tiling. Here, a tiling is a covering of the plane by non-overlapping polygons or other shapes, and a tiling is aperiodic if it does not contain arbitrarily large periodic regions or patches. However, despite their lack of translational symmetry, Penrose tilings may have both reflection symmetry and fivefold rotational symmetry. Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated them in the 1970s.
A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.
Lila Kari is a Romanian and Canadian computer scientist, professor in the David R. Cheriton School of Computer Science at the University of Waterloo, Canada.
A set of prototiles is aperiodic if copies of the prototiles can be assembled to create tilings, such that all possible tessellation patterns are non-periodic. The aperiodicity referred to is a property of the particular set of prototiles; the various resulting tilings themselves are just non-periodic.
In plane geometry, the einstein problem asks about the existence of a single prototile that by itself forms an aperiodic set of prototiles; that is, a shape that can tessellate space but only in a nonperiodic way. Such a shape is called an einstein, a word play on ein Stein, German for "one stone".
In geometry, a binary tiling is a tiling of the hyperbolic plane, resembling a quadtree over the Poincaré half-plane model of the hyperbolic plane. The tiles are congruent, each adjoining five others. They may be convex pentagons, or non-convex shapes with four sides, alternatingly line segments and horocyclic arcs, meeting at four right angles.
Craig S. Kaplan is a Canadian computer scientist, mathematician, and mathematical artist. He is an editor of the Journal of Mathematics and the Arts, and an organizer of the Bridges Conference on mathematics and art. He is an associate professor of computer science at the University of Waterloo, Canada.
| International | |
|---|---|
| National | |
| Academics | |
| Other | |
   | This article about a Finnish scientist is a stub. You can help Wikipedia by expanding it. |
 | This article about a European mathematician is a stub. You can help Wikipedia by expanding it. |
