
In geometry, an icosidodecahedron or pentagonal gyrobirotunda is a polyhedron with twenty (icosi-) triangular faces and twelve (dodeca-) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such, it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.
In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra.

In geometry, a polyhedron is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices.
In elementary geometry, a polytope is a geometric object with flat sides (faces). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions n as an n-dimensional polytope or n-polytope. For example, a two-dimensional polygon is a 2-polytope and a three-dimensional polyhedron is a 3-polytope. In this context, "flat sides" means that the sides of a (k + 1)-polytope consist of k-polytopes that may have (k – 1)-polytopes in common.
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. There are only five such polyhedra:

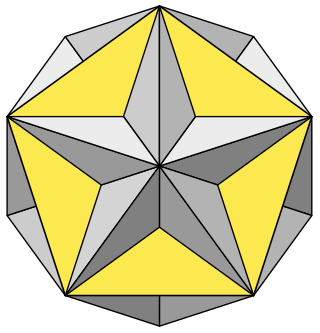
In geometry, stellation is the process of extending a polygon in two dimensions, a polyhedron in three dimensions, or, in general, a polytope in n dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word stellation comes from the Latin stellātus, "starred", which in turn comes from the Latin stella, "star". Stellation is the reciprocal or dual process to faceting.
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex.

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.
In geometry, a polytope or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in the same or reverse order, and with the same angles between corresponding faces.

In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general n-polytope is sliced off.

In geometry, the complete or final stellation of the icosahedron is the outermost stellation of the icosahedron, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram. That is, every three intersecting face planes of the icosahedral core intersect either on a vertex of this polyhedron or inside of it. It was studied by Max Brückner after the discovery of Kepler–Poinsot polyhedron. It can be viewed as an irregular, simple, and star polyhedron.

In geometry, an apeirogon or infinite polygon is a polygon with an infinite number of sides. Apeirogons are the rank 2 case of infinite polytopes. In some literature, the term "apeirogon" may refer only to the regular apeirogon, with an infinite dihedral group of symmetries.

In geometry, a skew polygon is a closed polygonal chain in Euclidean space. It is a figure similar to a polygon except its vertices are not all coplanar. While a polygon is ordinarily defined as a plane figure, the edges and vertices of a skew polygon form a space curve. Skew polygons must have at least four vertices. The interior surface and corresponding area measure of such a polygon is not uniquely defined.
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.
In geometry, a skew apeirohedron is an infinite skew polyhedron consisting of nonplanar faces or nonplanar vertex figures, allowing the figure to extend indefinitely without folding round to form a closed surface.

In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon in which every n – 1 consecutive sides belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a regular polyhedron is a skew polygon such that every two consecutive sides belongs to one of the faces. Petrie polygons are named for mathematician John Flinders Petrie.
In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedra which include the possibility of nonplanar faces or vertex figures. Coxeter looked at skew vertex figures which created new 4-dimensional regular polyhedra, and much later Branko Grünbaum looked at regular skew faces.

In geometry, the density of a star polyhedron is a generalization of the concept of winding number from two dimensions to higher dimensions, representing the number of windings of the polyhedron around the center of symmetry of the polyhedron. It can be determined by passing a ray from the center to infinity, passing only through the facets of the polytope and not through any lower dimensional features, and counting how many facets it passes through. For polyhedra for which this count does not depend on the choice of the ray, and for which the central point is not itself on any facet, the density is given by this count of crossed facets.

In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron. They have either skew regular faces or skew regular vertex figures.











