Kontsevich invariant

In the mathematical theory of knots, the Kontsevich invariant, also known as the Kontsevich integral ^[1] of an oriented framed link, is a universal Vassiliev invariant ^[2] in the sense that any coefficient of the Kontsevich invariant is of a finite type, and conversely any finite type invariant can be presented as a linear combination of such coefficients. It was defined by Maxim Kontsevich.

The Kontsevich invariant is a universal quantum invariant in the sense that any quantum invariant may be recovered by substituting the appropriate weight system into any Jacobi diagram.

Definition

The Kontsevich invariant is defined by monodromy along solutions of the Knizhnik–Zamolodchikov equations.

Jacobi diagram and Chord diagram

Definition

an example of a Jacobi diagram

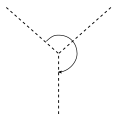
Let X be a circle (which is a 1-dimensional manifold). As is shown in the figure on the right, a Jacobi diagram with order n is the graph with 2n vertices, with the external circle depicted as solid line circle and with dashed lines called inner graph, which satisfies the following conditions:

1. The orientation is given only to the external circle.
2. The vertices have values 1 or 3. The valued 3 vertices are connected to one of the other edge with clockwise or anti-clockwise direction depicted as the little directed circle. The valued 1 vertices are connected to the external circle without multiplicity, ordered by the orientation of the circle.

The edges on G are called chords. We denote as A(X) the quotient space of the commutative group generated by all the Jacobi diagrams on X divided by the following relations:

(The AS relation) + = 0

(The IHX relation) = −

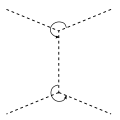(The STU relation) = −

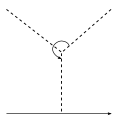(The FI relation) = 0.

A diagram without vertices valued 3 is called a chord diagram or Gauss diagram. If every connected component of a graph G has a vertex valued 3, then we can make the Jacobi diagram into a Chord diagram using the STU relation recursively. If we restrict ourselves only to chord diagrams, then the above four relations are reduced to the following two relations:

(The four term relation) − 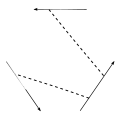+ 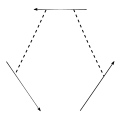− 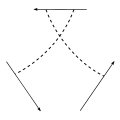= 0.

(The FI relation) = 0.

Properties

• The degree of a Jacobi diagram is defined to be the half of the sum of the number of its vertices with value 1 and one with value 3. It is the number of chords in the Chord diagram transformed from the Jacobi diagram.
• Just like for the tangles, the Jacobi diagrams form a monoidal category with the composition as the compiling of Jacobi diagrams along up and down direction and the tensor product as juxtapositioning Jacobi diagrams.
  • In the special case where X is an interval I, A(X) will be a commutative algebra. Viewing A(S¹) as the algebra with multiplication as connected sums, A(S¹) is isomorphic to A(I).
• A Jacobi diagram can be viewed as abstraction of representations of the tensor algebra generated by Lie algebras, which allows us to define some operations analogous to coproducts, counits and antipodes of Hopf algebras.
• Since the Vassiliev invariants (or finite type invariants) are closely related to chord diagrams, one can construct a singular knot from a chord diagram G on S¹. K_n denoting the space generated by all the singular knots with degree n, every such G determines a unique element in K_m / K_m+1.

Weight system

A map from the Jacobi diagrams to the positive integers is called a weight system. The map extended to the space A(X) is also called the weight system. They have the following properties:

• Let g be a semisimple Lie algebra and ρ its representation. We obtain a weight system by "substituting" the invariant tensor of g into the chord of a Jacobi diagram and ρ into the underlying manifold X of the Jacobi diagram.
  • We can view the vertices with value 3 of the Jacobi diagram as the bracket product of the Lie algebra, solid line arrows as the representation space of ρ, and the vertices with value 1 as the action of the Lie algebra.
  • The IHX relation and the STU relation correspond respectively to the Jacobi identity and the definition of the representation

ρ([a, b])v = ρ(a)ρ(b)v−ρ(b)ρ(a)v.

• Weight systems play an essential role in the proof of the Mervin-Morton conjecture, ^[3] which relates Alexander polynomials to Jones polynomials.

History

Jacobi diagrams were introduced as analogues of Feynman diagrams when Kontsevich defined knot invariants by iterated integrals in the first half of 1990s. ^[2] He represented singular points of singular knots by chords, i.e. he treated only with chord diagrams. D. Bar-Natan later formulated them as the 1-3 valued graphs and studied their algebraic properties, and called them "Chinese character diagrams" in his paper. ^[4] Several terms such as chord diagrams, web diagrams, or Feynman diagrams were used to refer them, but they have been called Jacobi diagrams since around 2000, because the IHX relation corresponds to the Jacobi identity for Lie algebras.

We can interpret them from a more general point of view by claspers, which were defined independently by Goussarov and Kazuo Habiro in the later half of the 1990s.

References

1. Chmutov, Sergei; Duzhi, Sergei (2012). Weisstein, Eric W (ed.). "Kontsevich Integral". Mathworld. Wolfram Web Resource. Retrieved 4 December 2012.
2. Kontsevich, Maxim (1993). "Vassiliev's knot invariants" (PDF). Adv. Soviet Math. 16 (2): 137–150.
3. Bar-Natan, D.; Garoufalidis, S. (1996). "On the Melvin-Morton-Rozansky Conjecture". Inventiones Mathematicae. 125: 103–133. doi:10.1007/s002220050070. S2CID   16891212.
4. Bar-Natan, D. (1995). "On the Vassiliev knot invariants". Topology. 34 (2): 423–472. doi: 10.1016/0040-9383(95)93237-2 .

Bibliography

• Ohtsuki, Tomotada (2001). Quantum Invariants – A Study of Knots, 3-Manifolds, and their Sets (1st ed.). World Scientific Publishing Company. ISBN   9789810246754. OL   9195378M.