In physical chemistry, the Arrhenius equation is a formula for the temperature dependence of reaction rates. The equation was proposed by Svante Arrhenius in 1889, based on the work of Dutch chemist Jacobus Henricus van 't Hoff who had noted in 1884 that the van 't Hoff equation for the temperature dependence of equilibrium constants suggests such a formula for the rates of both forward and reverse reactions. This equation has a vast and important application in determining the rate of chemical reactions and for calculation of energy of activation. Arrhenius provided a physical justification and interpretation for the formula. Currently, it is best seen as an empirical relationship. It can be used to model the temperature variation of diffusion coefficients, population of crystal vacancies, creep rates, and many other thermally-induced processes/reactions. The Eyring equation, developed in 1935, also expresses the relationship between rate and energy.
The process by which heat is transferred from the hotter end to the colder end of object is known as conduction.

In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region.
The Born–Haber cycle is an approach to analyze reaction energies. It was named after the two German scientists Max Born and Fritz Haber, who developed it in 1919. It was also independently formulated by Kasimir Fajans and published concurrently in the same issue of the same journal. The cycle is concerned with the formation of an ionic compound from the reaction of a metal with a halogen or other non-metallic element such as oxygen.
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant.
The Clausius–Clapeyron relation, named after Rudolf Clausius and Benoît Paul Émile Clapeyron, specifies the temperature dependence of pressure, most importantly vapor pressure, at a discontinuous phase transition between two phases of matter of a single constituent. Its relevance to climatology is the increase of the water-holding capacity of the atmosphere by about 7% for every 1 °C (1.8 °F) rise in temperature.
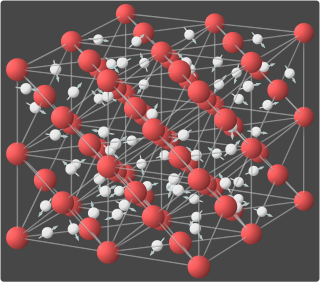
Atomic diffusion is a diffusion process whereby the random thermally-activated movement of atoms in a solid results in the net transport of atoms. For example, helium atoms inside a balloon can diffuse through the wall of the balloon and escape, resulting in the balloon slowly deflating. Other air molecules have lower mobilities and thus diffuse more slowly through the balloon wall. There is a concentration gradient in the balloon wall, because the balloon was initially filled with helium, and thus there is plenty of helium on the inside, but there is relatively little helium on the outside. The rate of transport is governed by the diffusivity and the concentration gradient.
Marcus theory is a theory originally developed by Rudolph A. Marcus, starting in 1956, to explain the rates of electron transfer reactions – the rate at which an electron can move or jump from one chemical species (called the electron donor) to another (called the electron acceptor). It was originally formulated to address outer sphere electron transfer reactions, in which the two chemical species only change in their charge with an electron jumping (e.g. the oxidation of an ion like Fe2+/Fe3+), but do not undergo large structural changes. It was extended to include inner sphere electron transfer contributions, in which a change of distances or geometry in the solvation or coordination shells of the two chemical species is taken into account (the Fe-O distances in Fe(H2O)2+ and Fe(H2O)3+ are different).
The Eyring equation is an equation used in chemical kinetics to describe changes in the rate of a chemical reaction against temperature. It was developed almost simultaneously in 1935 by Henry Eyring, Meredith Gwynne Evans and Michael Polanyi. The equation follows from the transition state theory, also known as activated-complex theory. If one assumes a constant enthalpy of activation and constant entropy of activation, the Eyring equation is similar to the empirical Arrhenius equation, despite the Arrhenius equation being empirical and the Eyring equation based on statistical mechanical justification.
In condensed matter physics and crystallography, the static structure factor is a mathematical description of how a material scatters incident radiation. The structure factor is a critical tool in the interpretation of scattering patterns obtained in X-ray, electron and neutron diffraction experiments.
Diffusion creep refers to the deformation of crystalline solids by the diffusion of vacancies through their crystal lattice. Diffusion creep results in plastic deformation rather than brittle failure of the material.

Coble creep, a form of diffusion creep, is a mechanism for deformation of crystalline solids. Contrasted with other diffusional creep mechanisms, Coble creep is similar to Nabarro–Herring creep in that it is dominant at lower stress levels and higher temperatures than creep mechanisms utilizing dislocation glide. Coble creep occurs through the diffusion of atoms in a material along grain boundaries. This mechanism is observed in polycrystals or along the surface in a single crystal, which produces a net flow of material and a sliding of the grain boundaries.

In chemistry, transition state theory (TST) explains the reaction rates of elementary chemical reactions. The theory assumes a special type of chemical equilibrium (quasi-equilibrium) between reactants and activated transition state complexes.
Diffusivity, mass diffusivity or diffusion coefficient is a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species. Diffusivity is encountered in Fick's law and numerous other equations of physical chemistry.
In materials science, segregation is the enrichment of atoms, ions, or molecules at a microscopic region in a materials system. While the terms segregation and adsorption are essentially synonymous, in practice, segregation is often used to describe the partitioning of molecular constituents to defects from solid solutions, whereas adsorption is generally used to describe such partitioning from liquids and gases to surfaces. The molecular-level segregation discussed in this article is distinct from other types of materials phenomena that are often called segregation, such as particle segregation in granular materials, and phase separation or precipitation, wherein molecules are segregated in to macroscopic regions of different compositions. Segregation has many practical consequences, ranging from the formation of soap bubbles, to microstructural engineering in materials science, to the stabilization of colloidal suspensions.
In electrochemistry, the Butler–Volmer equation, also known as Erdey-Grúz–Volmer equation, is one of the most fundamental relationships in electrochemical kinetics. It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction, considering that both a cathodic and an anodic reaction occur on the same electrode:

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition.
Dislocation creep is a deformation mechanism in crystalline materials. Dislocation creep involves the movement of dislocations through the crystal lattice of the material, in contrast to diffusion creep, in which diffusion is the dominant creep mechanism. It causes plastic deformation of the individual crystals, and thus the material itself.
In chemical thermodynamics, excess properties are properties of mixtures which quantify the non-ideal behavior of real mixtures. They are defined as the difference between the value of the property in a real mixture and the value that would exist in an ideal solution under the same conditions. The most frequently used excess properties are the excess volume, excess enthalpy, and excess chemical potential. The excess volume, internal energy, and enthalpy are identical to the corresponding mixing properties; that is,
Nabarro–Herring creep is a mode of deformation of crystalline materials that occurs at low stresses and held at elevated temperatures in fine-grained materials. In Nabarro–Herring creep, atoms diffuse through the crystals, and the creep rate varies inversely with the square of the grain size so fine-grained materials creep faster than coarser-grained ones. NH creep is solely controlled by diffusional mass transport. This type of creep results from the diffusion of vacancies from regions of high chemical potential at grain boundaries subjected to normal tensile stresses to regions of lower chemical potential where the average tensile stresses across the grain boundaries are zero. Self-diffusion within the grains of a polycrystalline solid can cause the solid to yield to an applied shearing stress, the yielding being caused by a diffusional flow of matter within each crystal grain away from boundaries where there is a normal pressure and toward those where there is a normal tension. Atoms migrating in the opposite direction account for the creep strain. The creep strain rate is derived in the next section. NH creep is more important in ceramics than metals as dislocation motion is more difficult to effect in ceramics.