A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

In geometry, a hypercube is an n-dimensional analogue of a square and a cube. It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to .
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by .

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.

In geometry, Pick's theorem provides a formula for the area of a simple polygon with integer vertex coordinates, in terms of the number of integer points within it and on its boundary. The result was first described by Georg Alexander Pick in 1899. It was popularized in English by Hugo Steinhaus in the 1950 edition of his book Mathematical Snapshots. It has multiple proofs, and can be generalized to formulas for certain kinds of non-simple polygons.
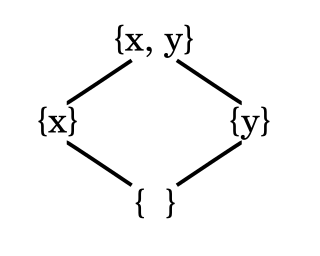
In order theory, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set one represents each element of as a vertex in the plane and draws a line segment or curve that goes upward from one vertex to another vertex whenever covers . These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.

In the mathematical discipline of graph theory, the dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In mathematics, the n-dimensional integer lattice, denoted , is the lattice in the Euclidean space whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. is the simplest example of a root lattice. The integer lattice is an odd unimodular lattice.

A regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes. Its opposite is irregular grid.

In graph theory, a knight's graph, or a knight's tour graph, is a graph that represents all legal moves of the knight chess piece on a chessboard. Each vertex of this graph represents a square of the chessboard, and each edge connects two squares that are a knight's move apart from each other. More specifically, an knight's graph is a knight's graph of an chessboard. Its vertices can be represented as the points of the Euclidean plane whose Cartesian coordinates are integers with and , and with two vertices connected by an edge when their Euclidean distance is .

In mathematics, particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points whenever the distance between them is exactly one. To distinguish these graphs from a broader definition that allows some non-adjacent pairs of vertices to be at distance one, they may also be called strict unit distance graphs or faithful unit distance graphs. As a hereditary family of graphs, they can be characterized by forbidden induced subgraphs. The unit distance graphs include the cactus graphs, the matchstick graphs and penny graphs, and the hypercube graphs. The generalized Petersen graphs are non-strict unit distance graphs.

In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and there is an edge between any two squares sharing a row (rank) or column (file), the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape. Although rook's graphs have only minor significance in chess lore, they are more important in the abstract mathematics of graphs through their alternative constructions: rook's graphs are the Cartesian product of two complete graphs, and are the line graphs of complete bipartite graphs. The square rook's graphs constitute the two-dimensional Hamming graphs.
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.
Heiko Harborth is Professor of Mathematics at Braunschweig University of Technology, 1975–present, and author of more than 188 mathematical publications. His work is mostly in the areas of number theory, combinatorics and discrete geometry, including graph theory.

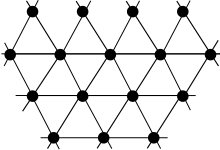
In geometric graph theory, a branch of mathematics, a matchstick graph is a graph that can be drawn in the plane in such a way that its edges are line segments with length one that do not cross each other. That is, it is a graph that has an embedding which is simultaneously a unit distance graph and a plane graph. For this reason, matchstick graphs have also been called planar unit-distance graphs. Informally, matchstick graphs can be made by placing noncrossing matchsticks on a flat surface, hence the name.
In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte (1963), states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.
In geometry, the distance set of a collection of points is the set of distances between distinct pairs of points. Thus, it can be seen as the generalization of a difference set, the set of distances in collections of numbers.

In graph theory, a locally linear graph is an undirected graph in which every edge belongs to exactly one triangle. Equivalently, for each vertex of the graph, its neighbors are each adjacent to exactly one other neighbor, so the neighbors can be paired up into an induced matching. Locally linear graphs have also been called locally matched graphs. Their triangles form the hyperedges of triangle-free 3-uniform linear hypergraphs and the blocks of certain partial Steiner triple systems, and the locally linear graphs are exactly the Gaifman graphs of these hypergraphs or partial Steiner systems.