
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commutative. With addition as an operation, the integers and the real numbers form abelian groups, and the concept of an abelian group may be viewed as a generalization of these examples. Abelian groups are named after Niels Henrik Abel.
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group.

In mathematics, specifically group theory, given a prime number p, a p-group is a group in which the order of every element is a power of p. That is, for each element g of a p-group G, there exists a nonnegative integer n such that the product of pn copies of g, and not fewer, is equal to the identity element. The orders of different elements may be different powers of p.

In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group defined over a finite set of symbols consists of the permutations that can be performed on the symbols. Since there are such permutation operations, the order of the symmetric group is .

In abstract algebra, a cyclic group or monogenous group is a group, denoted Cn, that is generated by a single element. That is, it is a set of invertible elements with a single associative binary operation, and it contains an element g such that every other element of the group may be obtained by repeatedly applying the group operation to g or its inverse. Each element can be written as an integer power of g in multiplicative notation, or as an integer multiple of g in additive notation. This element g is called a generator of the group.

In mathematics, specifically in the field of finite group theory, the Sylow theorems are a collection of theorems named after the Norwegian mathematician Peter Ludwig Sylow that give detailed information about the number of subgroups of fixed order that a given finite group contains. The Sylow theorems form a fundamental part of finite group theory and have very important applications in the classification of finite simple groups.

In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory and geometry.
In the theory of abelian groups, the torsion subgroupAT of an abelian group A is the subgroup of A consisting of all elements that have finite order. An abelian group A is called a torsion group if every element of A has finite order and is called torsion-free if every element of A except the identity is of infinite order.

In mathematics, specifically group theory, a nilpotent groupG is a group that has an upper central series that terminates with G. Equivalently, it has a central series of finite length or its lower central series terminates with {1}.

In group theory, the quaternion group Q8 (sometimes just denoted by Q) is a non-abelian group of order eight, isomorphic to the eight-element subset of the quaternions under multiplication. It is given by the group presentation

In group theory, a dicyclic group (notation Dicn or Q4n, ⟨n,2,2⟩) is a particular kind of non-abelian group of order 4n (n > 1). It is an extension of the cyclic group of order 2 by a cyclic group of order 2n, giving the name di-cyclic. In the notation of exact sequences of groups, this extension can be expressed as:
In mathematics, specifically group theory, the index of a subgroup H in a group G is the number of left cosets of H in G, or equivalently, the number of right cosets of H in G. The index is denoted or or . Because G is the disjoint union of the left cosets and because each left coset has the same size as H, the index is related to the orders of the two groups by the formula

A group is a set together with an associative operation that admits an identity element and such that there exists an inverse for every element.
In mathematics, more specifically in group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no non-trivial abelian quotients. In symbols, a perfect group is one such that G(1) = G, or equivalently one such that Gab = {1}.
In geometric topology, a field within mathematics, the obstruction to a homotopy equivalence of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion which is an element in the Whitehead group. These concepts are named after the mathematician J. H. C. Whitehead.
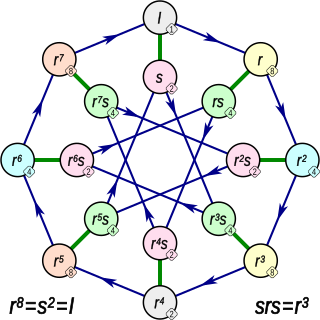
In mathematics, the quasi-dihedral groups, also called semi-dihedral groups, are certain non-abelian groups of order a power of 2. For every positive integer n greater than or equal to 4, there are exactly four isomorphism classes of non-abelian groups of order 2n which have a cyclic subgroup of index 2. Two are well known, the generalized quaternion group and the dihedral group. One of the remaining two groups is often considered particularly important, since it is an example of a 2-group of maximal nilpotency class. In Bertram Huppert's text Endliche Gruppen, this group is called a "Quasidiedergruppe". In Daniel Gorenstein's text, Finite Groups, this group is called the "semidihedral group". Dummit and Foote refer to it as the "quasidihedral group"; we adopt that name in this article. All give the same presentation for this group:

In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group of a group G. It was introduced by Issai Schur in his work on projective representations.
In mathematics, especially in the area of abstract algebra that studies infinite groups, the adverb virtually is used to modify a property so that it need only hold for a subgroup of finite index. Given a property P, the group G is said to be virtually P if there is a finite index subgroup such that H has property P.
In mathematics, or more specifically group theory, the omega and agemo subgroups described the so-called "power structure" of a finite p-group. They were introduced in where they were used to describe a class of finite p-groups whose structure was sufficiently similar to that of finite abelian p-groups, the so-called, regular p-groups. The relationship between power and commutator structure forms a central theme in the modern study of p-groups, as exemplified in the work on uniformly powerful p-groups.











