A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle. The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex; the shortest segment between the base and apex is the height. The area of a triangle equals one-half the product of height and base length.

In Euclidean plane geometry, a rectangle is a rectilinear convex polygon or a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.

In geometry, two geometric objects are perpendicular if their intersection forms right angles at the point of intersection called a foot. The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. Perpendicular intersections can happen between two lines, between a line and a plane, and between two planes.

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

In mathematics, affine geometry is what remains of Euclidean geometry when ignoring the metric notions of distance and angle.

In Euclidean geometry, a square is a regular quadrilateral, which means that it has four straight sides of equal length and four equal angles. It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°). A square with vertices ABCD would be denoted ABCD.
In geometry, parallel lines are coplanar infinite straight lines that do not intersect at any point. Parallel planes are planes in the same three-dimensional space that never meet. Parallel curves are curves that do not touch each other or intersect and keep a fixed minimum distance. In three-dimensional Euclidean space, a line and a plane that do not share a point are also said to be parallel. However, two noncoplanar lines are called skew lines. Line segments and Euclidean vectors are parallel if they have the same direction or opposite direction.

In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word line may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points.

In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.
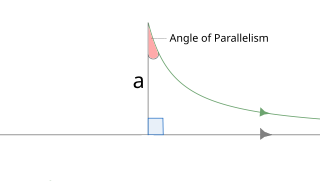
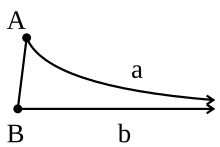
In hyperbolic geometry, angle of parallelism is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.
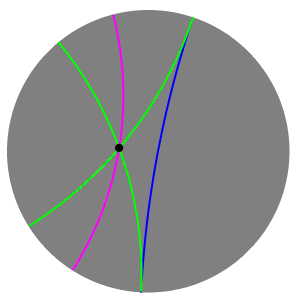
In hyperbolic geometry, two lines are said to be ultraparallel if they do not intersect and are not limiting parallel.

In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of hyperbolic geometry in which points are represented by the points in the interior of the unit disk and lines are represented by the chords, straight line segments with ideal endpoints on the boundary sphere.

In hyperbolic geometry, an ideal point, omega point or point at infinity is a well-defined point outside the hyperbolic plane or space. Given a line l and a point P not on l, right- and left-limiting parallels to l through P converge to l at ideal points.
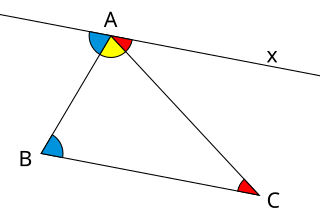
In a Euclidean space, the sum of angles of a triangle equals a straight angle. A triangle has three angles, one at each vertex, bounded by a pair of adjacent sides.
Ordered geometry is a form of geometry featuring the concept of intermediacy but, like projective geometry, omitting the basic notion of measurement. Ordered geometry is a fundamental geometry forming a common framework for affine, Euclidean, absolute, and hyperbolic geometry.
The exterior angle theorem is Proposition 1.16 in Euclid's Elements, which states that the measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. This is a fundamental result in absolute geometry because its proof does not depend upon the parallel postulate.
Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.

In geometry, Playfair's axiom is an axiom that can be used instead of the fifth postulate of Euclid :
In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the point.

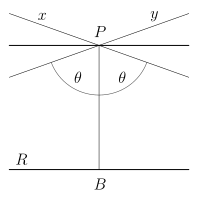
Hyperbolic geometry is a non-Euclidean geometry where the first four axioms of Euclidean geometry are kept but the fifth axiom, the parallel postulate, is changed. The fifth axiom of hyperbolic geometry says that given a line L and a point P not on that line, there are at least two lines passing through P that are parallel to L. As in Euclidean geometry, where ancient Greek mathematicians used a compass and idealized ruler for constructions of lengths, angles, and other geometric figures, constructions can also be made in hyperbolic geometry.