Horocycle

Last updated January 09, 2025

In hyperbolic geometry, a horocycle (from Greek roots meaning "boundary circle"), sometimes called an oricycle or limit circle, is a curve of constant curvature where all the perpendicular geodesics (normals) through a point on a horocycle are limiting parallel, and all converge asymptotically to a single ideal point called the centre of the horocycle. In some models of hyperbolic geometry it looks like the two "ends" of a horocycle get closer and closer to each other and closer to its centre, this is not true; the two "ends" of a horocycle get further and further away from each other and stay at an infinite distance off its centre. A horosphere is the 3-dimensional version of a horocycle.

Properties
Properties similar to those of Euclidean circles
Other properties
Horocycles in a hyperbolic plane with standardized Gaussian curvature
Representations in models of hyperbolic geometry
Poincaré disk model
Poincaré half-plane model
Hyperboloid model
Metric
Horocycle flow
See also
References
Further reading

In Euclidean space, all curves of constant curvature are either straight lines (geodesics) or circles, but in a hyperbolic space of sectional curvature $-1,$ the curves of constant curvature come in four types: geodesics with curvature $\kappa =0,$ hypercycles with curvature $0<|\kappa |<1,$ horocycles with curvature $|\kappa |=1,$ and circles with curvature $|\kappa |>1.$

Any two horocycles are congruent, and can be superimposed by an isometry (translation and rotation) of the hyperbolic plane.

A horocycle can also be described as the limit of the circles that share a tangent at a given point, as their radii tend to infinity, or as the limit of hypercycles tangent at the point as the distances from their axes tends to infinity.

Two horocycles with the same centre are called concentric . As for concentric circles, any geodesic perpendicular to a horocycle is also perpendicular to every concentric horocycle.

Properties

Properties similar to those of Euclidean circles

Horocycles in hyperbolic geometry have some properties similar to those of circles in Euclidean geometry:

No three points of a horocycle are on a line, circle or hypercycle.
Three points that are not on a line,circle or hypercycle are on a horocycle
A horocycle is a highly symmetric shape: every line through the centre forms a line of reflection symmetry.

A straight line, circle, hypercycle, or other horocycle cuts a horocycle in at most two points.
The length of an arc of a horocycle between two points is greater than that of the line segment between those two points.
The perpendicular bisector of a chord passes through the centre of the horocycle; equivalent statements stemming from the uniqueness of the perpendicular bisector are:

A perpendicular line from the centre of a horocycle bisects the chord.

The line segment through the centre bisecting a chord is perpendicular to the chord.

A line drawn perpendicular to a radius through the end point of the radius lying on the horocycle is a tangent to the horocycle.
A line drawn perpendicular to a tangent through the point of contact with a horocycle passes through the centre of the horocycle.
From a point outside the horocycle, two tangents can be drawn to the horocycle, and these tangents are equal in length.
The area of a sector of a horocycle (the area between two radii and the horocycle) is finite.^[1]
If C is the centre of a horocycle and A and B are points on the horocycle then the angles CAB and CBA are equal.^[2]

Other properties

Through every pair of points there are 2 horocycles. The centres of the horocycles are the ideal points of the perpendicular bisector of the segment between them.
All horocycles are congruent . (Even concentric horocycles are congruent to each other)
The length of an arc of a horocycle between two points is:

greater than the length of the line segment between those two points,

greater than the length of the arc of a hypercycle between those two points and

shorter than the length of any circle arc between those two points.

While the area of a sector of a horocycle is finite, the total area of a horocycle is infinite (a horocycle can be divided in an infinite number of equal sectors)
A regular apeirogon can be circumscribed and inscribed by two concentric horocycles.
The distance from a horocycle to its centre is infinite, and while in some models of hyperbolic geometry it looks like the two "ends" of a horocycle get closer and closer together and closer to its centre, this is not true; the two "ends" of a horocycle get further and further away from each other.

Horocycles in a hyperbolic plane with standardized Gaussian curvature

When the hyperbolic plane has the standardized Gaussian curvature K of -1:

The area of a sector of a horocycle is equal to the length of the arc subtending it.
The curvature of the horocycle is 1
The lengths of an arc of a horocycle between two points is: $s=2\sinh \left({\frac {1}{2}}d\right)={\sqrt {2(\cosh d-1)}}$

where d is the distance between the two points, and sinh and cosh are hyperbolic functions.^[3]

The length of an arc of a horocycle such that the tangent at one extremity is limiting parallel to the radius through the other extremity is 1.^[4] the area enclosed between this horocycle and the radii is 1.^[5]
The ratio of the arc lengths between two radii of two concentric horocycles where the horocycles are a distance 1 apart is e : 1.^[6]

Representations in models of hyperbolic geometry

Poincaré disk model

In the Poincaré disk model of the hyperbolic plane, horocycles are represented by circles tangent to the boundary circle; the centre of the horocycle is the ideal point where the horocycle touches the boundary circle.

The compass and straightedge construction of the two horocycles through two points is the same construction of the CPP construction for the Special cases of Apollonius' problem where both points are inside the circle.

In the Poincaré disk model, it looks like points near opposite "ends" of a horocycle get closer to each other and to the center of the horocycle (on the boundary circle), but in hyperbolic geometry every point on a horocycle is infinitely distant from the center of the horocycle. Also the distance between points on opposite "ends" of the horocycle increases as the arc length between those points increases. (The Euclidean intuition can be misleading because the scale of the model increases to infinity at the boundary circle.)

Poincaré half-plane model

In the Poincaré half-plane model, horocycles are represented by circles tangent to the boundary line, in which case their centre is the ideal point where the circle touches the boundary line.

When the centre of the horocycle is the ideal point at $y=\infty$ then the horocycle is a line parallel to the boundary line.

The compass and straightedge construction in the first case is the same construction as the LPP construction for the Special cases of Apollonius' problem.

Hyperboloid model

In the hyperboloid model horocycles are represented by intersections of the hyperboloid with planes that generate parabolas on the asymptotic cone (see conic sections " the cutting plane is parallel to exactly one generating line of the cone " ) The normal of the cutting plane is a null vector in three-dimensional Minkowski space.

Metric

If the metric is normalized to have Gaussian curvature −1, then the horocycle is a curve of geodesic curvature 1 at every point.

Horocycle flow

Every horocycle is the orbit of a unipotent subgroup of PSL(2,R) in the hyperbolic plane. Moreover, the displacement at unit speed along the horocycle tangent to a given unit tangent vector induces a flow on the unit tangent bundle of the hyperbolic plane. This flow is called the horocycle flow of the hyperbolic plane.

Identifying the unit tangent bundle with the group PSL(2,R), the horocycle flow is given by the right-action of the unipotent subgroup $U=\{u_{t},\,t\in \mathbb {R} \}$ , where: $u_{t}=\pm \left({\begin{array}{cc}1&t\\0&1\end{array}}\right).$ That is, the flow at time $t$ starting from a vector represented by $g\in \mathrm {PSL} _{2}(\mathbb {R} )$ is equal to $gu_{t}$ .

If $S$ is a hyperbolic surface its unit tangent bundle also supports a horocycle flow. If $S$ is uniformised as $S=\Gamma \backslash \mathbb {H} ^{2}$ the unit tangent bundle is identified with $\Gamma \backslash \mathrm {PSL} _{2}(\mathbb {R} )$ and the flow starting at $\Gamma g$ is given by $t\mapsto \Gamma gu_{t}$ . When $S$ is compact, or more generally when $\Gamma$ is a lattice, this flow is ergodic (with respect to the normalised Liouville measure). Moreover, in this setting Ratner's theorems describe very precisely the possible closures for its orbits.^[7]

Related Research Articles

<span class="mw-page-title-main">Circle</span> Simple curve of Euclidean geometry

A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a disc.

A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle. The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex; the shortest segment between the base and apex is the height. The area of a triangle equals one-half the product of height and base length.

<span class="mw-page-title-main">Curvature</span> Mathematical measure of how much a curve or surface deviates from flatness

In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or surface is contained in a larger space, curvature can be defined extrinsically relative to the ambient space. Curvature of Riemannian manifolds of dimension at least two can be defined intrinsically without reference to a larger space.

In geometry, a geodesic is a curve representing in some sense the locally shortest path (arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line".

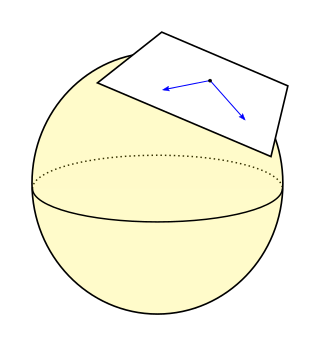
In differential geometry, a Riemannian manifold is a geometric space on which many geometric notions such as distance, angles, length, volume, and curvature are defined. Euclidean space, the $-sphere$ , hyperbolic space, and smooth surfaces in three-dimensional space, such as ellipsoids and paraboloids, are all examples of Riemannian manifolds. Riemannian manifolds are named after German mathematician Bernhard Riemann, who first conceptualized them.

<span class="mw-page-title-main">Hyperbolic geometry</span> type of non-Euclidean geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

In spherical geometry, a spherical circle is the locus of points on a sphere at constant spherical distance from a given point on the sphere. It is a curve of constant geodesic curvature relative to the sphere, analogous to a line or circle in the Euclidean plane; the curves analogous to straight lines are called great circles, and the curves analogous to planar circles are called small circles or lesser circles. If the sphere is embedded in three-dimensional Euclidean space, its circles are the intersections of the sphere with planes, and the great circles are intersections with planes passing through the center of the sphere.

In non-Euclidean geometry, the Poincaré half-plane model is a way of representing the hyperbolic plane using points in the familiar Euclidean plane. Specifically, each point in the hyperbolic plane is represented using a Euclidean point with coordinates ⁠ $⁠$ whose ⁠ $⁠$ coordinate is greater than zero, the upper half-plane, and a metric tensor called the Poincaré metric is adopted, in which the local scale is inversely proportional to the ⁠ $⁠$ coordinate. Points on the ⁠ $⁠$ -axis, whose ⁠ $⁠$ coordinate is equal to zero, represent ideal points, which are outside the hyperbolic plane proper.

This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology.

In geometry, hyperbolic motions are isometric automorphisms of a hyperbolic space. Under composition of mappings, the hyperbolic motions form a continuous group. This group is said to characterize the hyperbolic space. Such an approach to geometry was cultivated by Felix Klein in his Erlangen program. The idea of reducing geometry to its characteristic group was developed particularly by Mario Pieri in his reduction of the primitive notions of geometry to merely point and motion.

In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.

In mathematics, more particularly in the fields of dynamical systems and geometric topology, an Anosov map on a manifold M is a certain type of mapping, from M to itself, with rather clearly marked local directions of "expansion" and "contraction". Anosov systems are a special case of Axiom A systems.

In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of hyperbolic geometry in which points are represented by the points in the interior of the unit disk and lines are represented by the chords, straight line segments with ideal endpoints on the boundary sphere.

In hyperbolic geometry, an ideal point, omega point or point at infinity is a well-defined point outside the hyperbolic plane or space. Given a line l and a point P not on l, right- and left-limiting parallels to l through P converge to l at ideal points.

In hyperbolic geometry, a hypercycle, hypercircle or equidistant curve is a curve whose points have the same orthogonal distance from a given straight line.

In hyperbolic geometry, a horosphere is a specific hypersurface in hyperbolic n-space. It is the boundary of a horoball, the limit of a sequence of increasing balls sharing a tangent hyperplane and its point of tangency. For n = 2 a horosphere is called a horocycle.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric.

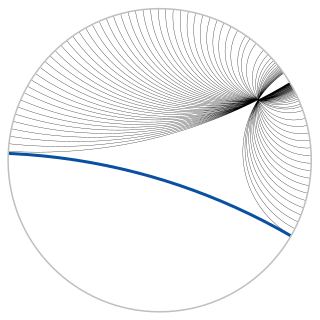
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk that are orthogonal to the unit circle or diameters of the unit circle.

In the hyperbolic plane, as in the Euclidean plane, each point can be uniquely identified by two real numbers. Several qualitatively different ways of coordinatizing the plane in hyperbolic geometry are used.

<span class="mw-page-title-main">Constructions in hyperbolic geometry</span>

Hyperbolic geometry is a non-Euclidean geometry where the first four axioms of Euclidean geometry are kept but the fifth axiom, the parallel postulate, is changed. The fifth axiom of hyperbolic geometry says that given a line L and a point P not on that line, there are at least two lines passing through P that are parallel to L. As in Euclidean geometry, where ancient Greek mathematicians used a compass and idealized ruler for constructions of lengths, angles, and other geometric figures, constructions can also be made in hyperbolic geometry.

References

↑ Coxeter, H.S.M. (1998). Non-Euclidean geometry (6. ed.). Washington, DC: Mathematical Assoc. of America. pp. 243 244. ISBN 978-0-88385-522-5.
↑ Sossinsky, A.B. (2012). Geometries. Providence, R.I.: American Mathematical Society. pp. 141 2. ISBN 9780821875711.
↑ Smogorzhevsky (1976). Lobachevskian Geometry. Moscow: Mir. p. 65.
↑ Sommerville, D.M.Y. (2005). The elements of non-Euclidean geometry (Unabr. and unaltered republ. ed.). Mineola, N.Y.: Dover Publications. p. 58. ISBN 0-486-44222-5.
↑ Coxeter, H.S.M. (1998). Non-Euclidean geometry (6. ed.). Washington, DC: Mathematical Assoc. of America. p. 250. ISBN 978-0-88385-522-5.
↑ Sommerville, D.M.Y. (2005). The elements of non-Euclidean geometry (Unabr. and unaltered republ. ed.). Mineola, N.Y.: Dover Publications. p. 58. ISBN 0-486-44222-5.
↑ Morris, Dave Witte (2005). Ratner's Theorems on Unipotent Flows. Chicago Lectures in Mathematics. Chicago, IL: University of Chicago Press. arXiv: math/0310402 . ISBN 978-0-226-53984-3. MR 2158954.