Related Research Articles

Paul Adrien Maurice Dirac was an English mathematical and theoretical physicist who is considered to be one of the founders of quantum mechanics and quantum electrodynamics. He is credited with laying the foundations of quantum field theory. He was the Lucasian Professor of Mathematics at the University of Cambridge, a professor of physics at Florida State University and the University of Miami, and a 1933 Nobel Prize in Physics recipient.

In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles.
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way.
In physics, charge conjugation is a transformation that switches all particles with their corresponding antiparticles, thus changing the sign of all charges: not only electric charge but also the charges relevant to other forces. The term C-symmetry is an abbreviation of the phrase "charge conjugation symmetry", and is used in discussions of the symmetry of physical laws under charge-conjugation. Other important discrete symmetries are P-symmetry (parity) and T-symmetry.
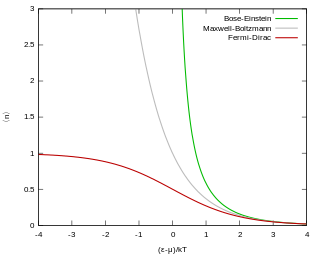
Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics.

In particle physics, a magnetic monopole is a hypothetical elementary particle that is an isolated magnet with only one magnetic pole. A magnetic monopole would have a net north or south "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring theories, which predict their existence. The known elementary particles that have electric charge are electric monopoles.
In physics, screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases, electrolytes, and charge carriers in electronic conductors . In a fluid, with a given permittivity ε, composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force as

The Dirac sea is a theoretical model of the electron vacuum as an infinite sea of electrons with negative energy, now called positrons. It was first postulated by the British physicist Paul Dirac in 1930 to explain the anomalous negative-energy quantum states predicted by the Dirac equation for relativistic electrons. The positron, the antimatter counterpart of the electron, was originally conceived of as a hole in the Dirac sea, before its experimental discovery in 1932.

In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology.
In mathematics, generalized functions are objects extending the notion of functions. There is more than one recognized theory, for example the theory of distributions. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing discrete physical phenomena such as point charges. They are applied extensively, especially in physics and engineering.

In particle physics, the history of quantum field theory starts with its creation by Paul Dirac, when he attempted to quantize the electromagnetic field in the late 1920s. Major advances in the theory were made in the 1940s and 1950s, leading to the introduction of renormalized quantum electrodynamics (QED). The field theory behind QED was so accurate and successful in predictions that efforts were made to apply the same basic concepts for the other forces of nature. Beginning in 1954, the parallel was found by way of gauge theory, leading by the late 1970s, to quantum field models of strong nuclear force and weak nuclear force, united in the modern Standard Model of particle physics.
Asım Orhan Barut was a Turkish-American theoretical physicist.
The history of mathematical notation includes the commencement, progress, and cultural diffusion of mathematical symbols and the conflict of the methods of notation confronted in a notation's move to popularity or inconspicuousness. Mathematical notation comprises the symbols used to write mathematical equations and formulas. Notation generally implies a set of well-defined representations of quantities and symbols operators. The history includes Hindu–Arabic numerals, letters from the Roman, Greek, Hebrew, and German alphabets, and a host of symbols invented by mathematicians over the past several centuries.

Giorgio Parisi is an Italian theoretical physicist, whose research has focused on quantum field theory, statistical mechanics and complex systems. His best known contributions are the QCD evolution equations for parton densities, obtained with Guido Altarelli, known as the Altarelli–Parisi or DGLAP equations, the exact solution of the Sherrington–Kirkpatrick model of spin glasses, the Kardar–Parisi–Zhang equation describing dynamic scaling of growing interfaces, and the study of whirling flocks of birds. He was awarded the 2021 Nobel Prize in Physics jointly with Klaus Hasselmann and Syukuro Manabe for groundbreaking contributions to theory of complex systems, in particular "for the discovery of the interplay of disorder and fluctuations in physical systems from atomic to planetary scales".
Pierre Ramond is distinguished professor of physics at University of Florida in Gainesville, Florida. He initiated the development of superstring theory.
Paul Dirac (1902–1984) was a Swiss-British theoretical physicist, Nobel laureate, and a founder of the field of quantum physics.
This page is a glossary of terms in string theory, including related areas such as supergravity, supersymmetry, and high energy physics.
References
- ↑ "Distributed Research utilising Advanced Computing (DiRAC)". dirac.ac.uk.