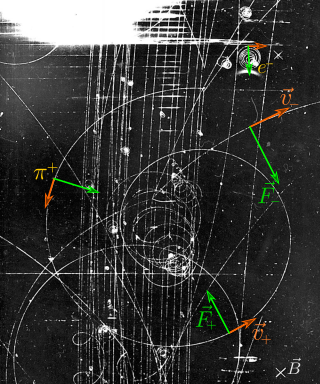
In physics, the Lorentz force is the combination of electric and magnetic force on a point charge due to electromagnetic fields. A particle of charge q moving with a velocity v in an electric field E and a magnetic field B experiences a force of

A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, electric currents, and electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, called a vector field.

Magnetohydrodynamics is a model of electrically conducting fluids that treats all interpenetrating particle species together as a single continuous medium. It is primarily concerned with the low-frequency, large-scale, magnetic behavior in plasmas and liquid metals and has applications in numerous fields including geophysics, astrophysics, and engineering.

In physics, specifically electromagnetism, the Biot–Savart law is an equation describing the magnetic field generated by a constant electric current. It relates the magnetic field to the magnitude, direction, length, and proximity of the electric current.

In special relativity, a four-vector is an object with four components, which transform in a specific way under Lorentz transformations. Specifically, a four-vector is an element of a four-dimensional vector space considered as a representation space of the standard representation of the Lorentz group, the representation. It differs from a Euclidean vector in how its magnitude is determined. The transformations that preserve this magnitude are the Lorentz transformations, which include spatial rotations and boosts.

In electromagnetism, the magnetic moment is the magnetic strength and orientation of a magnet or other object that produces a magnetic field. The magnetic moment is typically expressed as a vector. Examples of objects that have magnetic moments include loops of electric current, permanent magnets, elementary particles, composite particles, various molecules, and many astronomical objects.

In electromagnetism, displacement current density is the quantity ∂D/∂t appearing in Maxwell's equations that is defined in terms of the rate of change of D, the electric displacement field. Displacement current density has the same units as electric current density, and it is a source of the magnetic field just as actual current is. However it is not an electric current of moving charges, but a time-varying electric field. In physical materials, there is also a contribution from the slight motion of charges bound in atoms, called dielectric polarization.
A classical field theory is a physical theory that predicts how one or more physical fields interact with matter through field equations, without considering effects of quantization; theories that incorporate quantum mechanics are called quantum field theories. In most contexts, 'classical field theory' is specifically intended to describe electromagnetism and gravitation, two of the fundamental forces of nature.
In differential geometry, the four-gradient is the four-vector analogue of the gradient from vector calculus.
In electromagnetism, the Lorenz gauge condition or Lorenz gauge is a partial gauge fixing of the electromagnetic vector potential by requiring The name is frequently confused with Hendrik Lorentz, who has given his name to many concepts in this field. The condition is Lorentz invariant. The Lorenz gauge condition does not completely determine the gauge: one can still make a gauge transformation where is the four-gradient and is any harmonic scalar function: that is, a scalar function obeying the equation of a massless scalar field.

Stokes flow, also named creeping flow or creeping motion, is a type of fluid flow where advective inertial forces are small compared with viscous forces. The Reynolds number is low, i.e. . This is a typical situation in flows where the fluid velocities are very slow, the viscosities are very large, or the length-scales of the flow are very small. Creeping flow was first studied to understand lubrication. In nature, this type of flow occurs in the swimming of microorganisms and sperm. In technology, it occurs in paint, MEMS devices, and in the flow of viscous polymers generally.

A force-free magnetic field is a magnetic field in which the Lorentz force is equal to zero and the magnetic pressure greatly exceeds the plasma pressure such that non-magnetic forces can be neglected. For a force-free field, the electric current density is either zero or parallel to the magnetic field.
The Grad–Shafranov equation is the equilibrium equation in ideal magnetohydrodynamics (MHD) for a two dimensional plasma, for example the axisymmetric toroidal plasma in a tokamak. This equation takes the same form as the Hicks equation from fluid dynamics. This equation is a two-dimensional, nonlinear, elliptic partial differential equation obtained from the reduction of the ideal MHD equations to two dimensions, often for the case of toroidal axisymmetry. Taking as the cylindrical coordinates, the flux function is governed by the equation,

The Maxwell stress tensor is a symmetric second-order tensor used in classical electromagnetism to represent the interaction between electromagnetic forces and mechanical momentum. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impractically difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand.

In physics, magnetic pressure is an energy density associated with a magnetic field. In SI units, the energy density of a magnetic field with strength can be expressed as

A flux tube is a generally tube-like (cylindrical) region of space containing a magnetic field, B, such that the cylindrical sides of the tube are everywhere parallel to the magnetic field lines. It is a graphical visual aid for visualizing a magnetic field. Since no magnetic flux passes through the sides of the tube, the flux through any cross section of the tube is equal, and the flux entering the tube at one end is equal to the flux leaving the tube at the other. Both the cross-sectional area of the tube and the magnetic field strength may vary along the length of the tube, but the magnetic flux inside is always constant.
In magnetohydrodynamics (MHD), shocks and discontinuities are transition layers where properties of a plasma change from one equilibrium state to another. The relation between the plasma properties on both sides of a shock or a discontinuity can be obtained from the conservative form of the MHD equations, assuming conservation of mass, momentum, energy and of .

There are various mathematical descriptions of the electromagnetic field that are used in the study of electromagnetism, one of the four fundamental interactions of nature. In this article, several approaches are discussed, although the equations are in terms of electric and magnetic fields, potentials, and charges with currents, generally speaking.
In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-½ particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non-relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927.
In mathematical physics, the Gordon decomposition of the Dirac current is a splitting of the charge or particle-number current into a part that arises from the motion of the center of mass of the particles and a part that arises from gradients of the spin density. It makes explicit use of the Dirac equation and so it applies only to "on-shell" solutions of the Dirac equation.




























