Median of the Trapezoid theorem

Median of the Trapezoid theorem
	A trapezoid with the minimum necessary labeling.
Type	Geometry
Statement	The length of the median of a trapezoid is the average of the lengths of the two bases.

Last updated October 23, 2024

The Median of the Trapezoid theorem states that the median of a trapezoid is equal in length to the average of the lengths of the two bases.^[1] This theorem is a fundamental concept in geometry and has various applications in mathematics, particularly in the study of quadrilaterals.

Statement

Given a trapezoid ABCD, with bases AB and CD, the median (or midsegment) EF is the segment that joins the midpoints of the non-parallel sides AD and BC. The theorem asserts that the length of the median EF is equal to the average of the lengths of the two bases AB and CD. Mathematically, this is expressed as: $EF={\frac {AB+CD}{2}}$

Proof

Construction proof

The simplest proof that one can obtain is done by some extra construction.

Let ABCD be a trapezoid ( $AD\parallel BC,AD>BC$ ). Construct $E$ on $AD$ such that $BC=ED$ (and, therefore, $BCDE$ is a parallelogram). Let $M,P,N$ be the midpoints of $AB,BE$ and $CD$ respectively.

Since $BCDE$ is a parallelogram, $PN=BC$ . Using the midpoint theorem,

MP={\frac {1}{2}}AE.

Since $AE=AD-BC,$

MP={\frac {AD-BC}{2}}.

Summing this with $PN$ , we get

MN={\frac {AD+BC}{2}},

Q.E.D.

Coordinate geometry proof

Consider trapezoid ABCD in a coordinate plane, with vertices A(x₁, y₁), B(x₂, y₁), C(x₃, y₂), and D(x₄, y₂), where AB is parallel to CD. The midpoints of AD and BC are given by: $E=\left({\frac {x_{1}+x_{4}}{2}},{\frac {y_{1}+y_{2}}{2}}\right)$ and $F=\left({\frac {x_{2}+x_{3}}{2}},{\frac {y_{1}+y_{2}}{2}}\right)$

The length of the median EF is then calculated as: $EF={\sqrt {\left({\frac {x_{2}+x_{3}}{2}}-{\frac {x_{1}+x_{4}}{2}}\right)^{2}+\left({\frac {y_{1}+y_{2}}{2}}-{\frac {y_{1}+y_{2}}{2}}\right)^{2}}}={\frac {|x_{2}-x_{1}+x_{3}-x_{4}|}{2}}$

Since AB and CD are parallel, the distance between the x-coordinates of AB and CD is constant, and the length of EF is the average of AB and CD.

Applications

The Median of the Trapezoid theorem is widely used in solving geometric problems involving trapezoids. It simplifies the calculations of distances and areas in problems where trapezoids are involved.

Area of a trapezoid

One direct application is in deriving the formula for the area of a trapezoid. The area can be calculated as the product of the median and the height (the perpendicular distance between the bases): ${\text{Area}}=EF\times {\text{Height}}$

Historical context

The study of trapezoids and their properties has a long history in geometry, with the Median of the Trapezoid theorem being one of the key results. The theorem, which states that the median of a trapezoid is equal to the average of the lengths of the two bases, plays a fundamental role in understanding the geometry of trapezoids. Historically, trapezoids and their properties have been studied by mathematicians for centuries, with early references to the shapes and their characteristics found in ancient Greek mathematics. The Median of the Trapezoid theorem itself is an example of how simple geometric principles can yield powerful results, and it has been utilized in various mathematical applications and proofs throughout history. According to Howard Eves, a prominent historian of mathematics, the study of quadrilaterals like the trapezoid has contributed significantly to the development of geometry as a whole.^[2] The Median of the Trapezoid theorem, in particular, exemplifies the elegance and simplicity that can be found in geometric theorems, making it a notable topic of study in mathematical education and research.

Related concepts

Related Research Articles

In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices $,, and is sometimes denoted as .$

<span class="mw-page-title-main">Bisection</span> Division of something into two equal or congruent parts

In geometry, bisection is the division of something into two equal or congruent parts. Usually it involves a bisecting line, also called a bisector. The most often considered types of bisectors are the segment bisector, a line that passes through the midpoint of a given segment, and the angle bisector, a line that passes through the apex of an angle . In three-dimensional space, bisection is usually done by a bisecting plane, also called the bisector.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

<span class="mw-page-title-main">Trapezoid</span> Convex quadrilateral with at least one pair of parallel sides

In geometry, a trapezoid in North American English, or trapezium in British English, is a quadrilateral that has one pair of parallel sides.

In geometry, Thales's theorem states that if $A$ , $B$ , and $C$ are distinct points on a circle where the line $AC$ is a diameter, the angle $∠ ABC$ is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

<span class="mw-page-title-main">Midpoint</span> Point on a line segment which is equidistant from both endpoints

In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.

In Euclidean geometry, an isosceles trapezoid is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined as a trapezoid in which both legs and both base angles are of equal measure, or as a trapezoid whose diagonals have equal length. Note that a non-rectangular parallelogram is not an isosceles trapezoid because of the second condition, or because it has no line of symmetry. In any isosceles trapezoid, two opposite sides are parallel, and the two other sides are of equal length, and the diagonals have equal length. The base angles of an isosceles trapezoid are equal in measure.

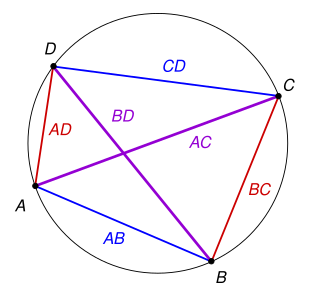
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral. The theorem is named after the Greek astronomer and mathematician Ptolemy. Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.

In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".

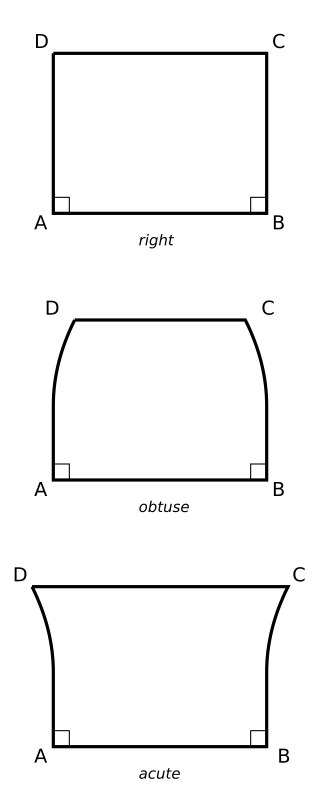
A Saccheri quadrilateral is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his 1733 book Euclides ab omni naevo vindicatus, an attempt to prove the parallel postulate using the method reductio ad absurdum. Such a quadrilateral is sometimes called a Khayyam–Saccheri quadrilateral to credit Persian scholar Omar Khayyam who described them in his 11th century book Risāla fī šarḥ mā aškala min muṣādarāt kitāb Uqlīdis.

In Euclidean geometry, the British flag theorem says that if a point P is chosen inside a rectangle ABCD then the sum of the squares of the Euclidean distances from P to two opposite corners of the rectangle equals the sum to the other two opposite corners. As an equation:

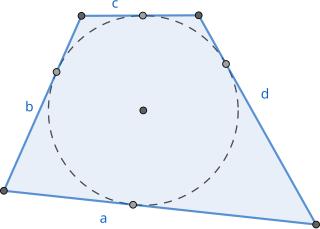
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all can be tangent to a single circle within the quadrilateral. This circle is called the incircle of the quadrilateral or its inscribed circle, its center is the incenter and its radius is called the inradius. Since these quadrilaterals can be drawn surrounding or circumscribing their incircles, they have also been called circumscribable quadrilaterals, circumscribing quadrilaterals, and circumscriptible quadrilaterals. Tangential quadrilaterals are a special case of tangential polygons.

In Euclidean geometry, Varignon's theorem holds that the midpoints of the sides of an arbitrary quadrilateral form a parallelogram, called the Varignon parallelogram. It is named after Pierre Varignon, whose proof was published posthumously in 1731.

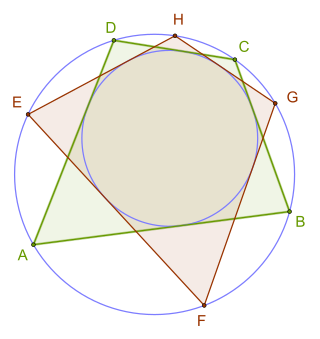
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. The radii and centers of these circles are called inradius and circumradius, and incenter and circumcenter respectively. From the definition it follows that bicentric quadrilaterals have all the properties of both tangential quadrilaterals and cyclic quadrilaterals. Other names for these quadrilaterals are chord-tangent quadrilateral and inscribed and circumscribed quadrilateral. It has also rarely been called a double circle quadrilateral and double scribed quadrilateral.

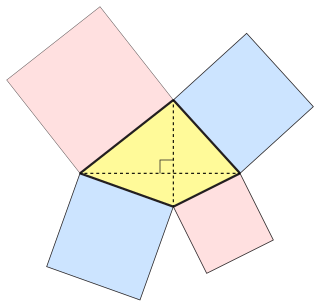
In Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal (perpendicular) to each other.

In Euclidean geometry, an ex-tangential quadrilateral is a convex quadrilateral where the extensions of all four sides are tangent to a circle outside the quadrilateral. It has also been called an exscriptible quadrilateral. The circle is called its excircle, its radius the exradius and its center the excenter. The excenter lies at the intersection of six angle bisectors. These are the internal angle bisectors at two opposite vertex angles, the external angle bisectors at the other two vertex angles, and the external angle bisectors at the angles formed where the extensions of opposite sides intersect. The ex-tangential quadrilateral is closely related to the tangential quadrilateral.

In Euclidean geometry, a tangential trapezoid, also called a circumscribed trapezoid, is a trapezoid whose four sides are all tangent to a circle within the trapezoid: the incircle or inscribed circle. It is the special case of a tangential quadrilateral in which at least one pair of opposite sides are parallel. As for other trapezoids, the parallel sides are called the bases and the other two sides the legs. The legs can be equal, but they don't have to be.

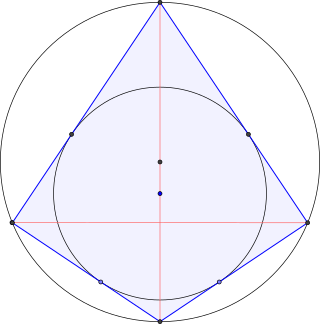
In Euclidean geometry, a right kite is a kite that can be inscribed in a circle. That is, it is a kite with a circumcircle. Thus the right kite is a convex quadrilateral and has two opposite right angles. If there are exactly two right angles, each must be between sides of different lengths. All right kites are bicentric quadrilaterals, since all kites have an incircle. One of the diagonals divides the right kite into two right triangles and is also a diameter of the circumcircle.

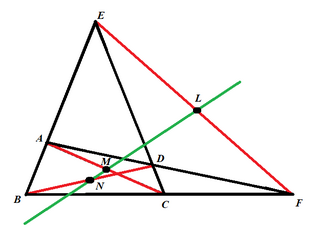
In geometry, the Newton–Gauss line is the line joining the midpoints of the three diagonals of a complete quadrilateral.

The midpoint theorem, midsegment theorem, or midline theorem states that if the midpoints of two sides of a triangle are connected, then the resulting line segment will be parallel to the third side and have half of its length. The midpoint theorem generalizes to the intercept theorem, where rather than using midpoints, both sides are partitioned in the same ratio.

References

↑ HOLT MCDOUGAL (2011-06-14). Holt McDougal Geometry: Student Edition 2012. Internet Archive. Holt McDougal. ISBN 978-0-547-64709-8.
↑ Eves, Howard (1990). An Introduction to the History of Mathematics. Saunders College Pub. ISBN 978-0-03-029558-4.

External links

Median of Trapezoid Explanation and Visualization

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] HOLT MCDOUGAL (2011-06-14). Holt McDougal Geometry: Student Edition 2012. Internet Archive. Holt McDougal. ISBN 978-0-547-64709-8.

[2] Eves, Howard (1990). An Introduction to the History of Mathematics. Saunders College Pub. ISBN 978-0-03-029558-4.

[1]

[2]