Mergelyan's theorem

Last updated June 24, 2024

Mergelyan's theorem is a result from approximation by polynomials in complex analysis proved by the Armenian mathematician Sergei Mergelyan in 1951.

Statement

Let

K

be a compact subset of the complex plane

\mathbb {C}

such that

\mathbb {C} \setminus K

is connected. Then, every continuous function

f:K\to \mathbb {C}

, such that the restriction

f

to

{\text{int}}(K)

is holomorphic, can be approximated uniformly on

K

with polynomials. Here,

{\text{int}}(K)

denotes the interior of

K

.^[1]^[2]

Mergelyan's theorem also holds for open Riemann surfaces

If

K

is a compact set without holes in an open Riemann surface

X

, then every function in

{\mathcal {A}}(K)

can be approximated uniformly on

K

by functions in

{\mathcal {O}}(X)

.^[2]

Mergelyan's theorem does not always hold in higher dimensions (spaces of several complex variables), but it has some consequences.^[2]

History

Mergelyan's theorem is a generalization of the Weierstrass approximation theorem and Runge's theorem.

In the case that $\mathbb {C} \setminus K$ is not connected, in the initial approximation problem the polynomials have to be replaced by rational functions. An important step of the solution of this further rational approximation problem was also suggested by Mergelyan in 1952. Further deep results on rational approximation are due to, in particular, A. G. Vitushkin.

Weierstrass and Runge's theorems were put forward in 1885, while Mergelyan's theorem dates from 1951. After Weierstrass and Runge, many mathematicians (in particular Walsh, Keldysh, Lavrentyev, Hartogs, and Rosenthal) had been working on the same problem. The method of the proof suggested by Mergelyan is constructive, and remains the only known constructive proof of the result.^{[ citation needed ]}

Related Research Articles

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, and applied mathematics, as well as in physics, including the branches of hydrodynamics, thermodynamics, quantum mechanics, and twistor theory. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering.

In complex analysis, the Riemann mapping theorem states that if $is a non-empty simply connected open subset of the complex number plane which is not all of, then there exists a biholomorphic mapping from onto the open unit disk$

In mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on a closed interval $[a, b]$ can be uniformly approximated as closely as desired by a polynomial function. Because polynomials are among the simplest functions, and because computers can directly evaluate polynomials, this theorem has both practical and theoretical relevance, especially in polynomial interpolation. The original version of this result was established by Karl Weierstrass in 1885 using the Weierstrass transform.

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally hold for real analytic functions.

In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where the infinite series representation which initially defined the function becomes divergent.

In mathematics, complex geometry is the study of geometric structures and constructions arising out of, or described by, the complex numbers. In particular, complex geometry is concerned with the study of spaces such as complex manifolds and complex algebraic varieties, functions of several complex variables, and holomorphic constructions such as holomorphic vector bundles and coherent sheaves. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric aspects of complex analysis.

The Riemann–Roch theorem is an important theorem in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeros and allowed poles. It relates the complex analysis of a connected compact Riemann surface with the surface's purely topological genus g, in a way that can be carried over into purely algebraic settings.

In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation $h (x, y, t) = 0$ can be restricted to the affine algebraic plane curve of equation $h (x, y, 1) = 0$ . These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.

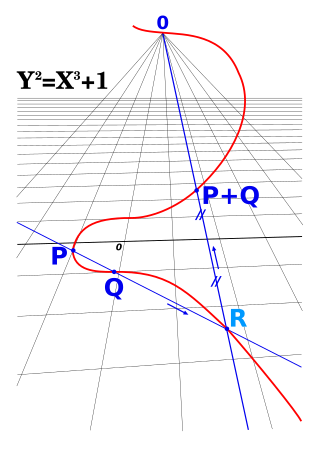
In algebraic geometry, a projective variety over an algebraically closed field k is a subset of some projective n-space $over k that is the zero-locus of some finite family of homogeneous polynomials of n + 1 variables with coefficients in k, that generate a prime ideal, the defining ideal of the variety. Equivalently, an algebraic variety is projective if it can be embedded as a Zariski closed subvariety of .$

The theory of functions of several complex variables is the branch of mathematics dealing with functions defined on the complex coordinate space $, that is, n -tuples of complex numbers. The name of the field dealing with the properties of these functions is called several complex variables, which the Mathematics Subject Classification has as a top-level heading.$

In mathematics, in the theory of several complex variables and complex manifolds, a Stein manifold is a complex submanifold of the vector space of n complex dimensions. They were introduced by and named after Karl Stein. A Stein space is similar to a Stein manifold but is allowed to have singularities. Stein spaces are the analogues of affine varieties or affine schemes in algebraic geometry.

In complex analysis, an area of mathematics, Montel's theorem refers to one of two theorems about families of holomorphic functions. These are named after French mathematician Paul Montel, and give conditions under which a family of holomorphic functions is normal.

Algebraic geometry codes, often abbreviated AG codes, are a type of linear code that generalize Reed–Solomon codes. The Russian mathematician V. D. Goppa constructed these codes for the first time in 1982.

In mathematics, the Hirzebruch–Riemann–Roch theorem, named after Friedrich Hirzebruch, Bernhard Riemann, and Gustav Roch, is Hirzebruch's 1954 result generalizing the classical Riemann–Roch theorem on Riemann surfaces to all complex algebraic varieties of higher dimensions. The result paved the way for the Grothendieck–Hirzebruch–Riemann–Roch theorem proved about three years later.

In complex analysis, Runge's theorem is named after the German mathematician Carl Runge who first proved it in the year 1885. It states the following:

In mathematics, the Oka coherence theorem, proved by Kiyoshi Oka, states that the sheaf $of holomorphic functions on is coherent.$

In mathematics, the Hartogs–Rosenthal theorem is a classical result in complex analysis on the uniform approximation of continuous functions on compact subsets of the complex plane by rational functions. The theorem was proved in 1931 by the German mathematicians Friedrich Hartogs and Arthur Rosenthal and has been widely applied, particularly in operator theory.

In mathematics, the Farrell–Markushevich theorem, proved independently by O. J. Farrell (1899–1981) and A. I. Markushevich (1908–1979) in 1934, is a result concerning the approximation in mean square of holomorphic functions on a bounded open set in the complex plane by complex polynomials. It states that complex polynomials form a dense subspace of the Bergman space of a domain bounded by a simple closed Jordan curve. The Gram–Schmidt process can be used to construct an orthonormal basis in the Bergman space and hence an explicit form of the Bergman kernel, which in turn yields an explicit Riemann mapping function for the domain.

In mathematics, especially the theory of several complex variables, the Oka–Weil theorem is a result about the uniform convergence of holomorphic functions on Stein spaces due to Kiyoshi Oka and André Weil.

References

Lennart Carleson, Mergelyan's theorem on uniform polynomial approximation, Math. Scand., V. 15, (1964) 167–175.
Dieter Gaier, Lectures on Complex Approximation, Birkhäuser Boston, Inc. (1987), ISBN 0-8176-3147-X.
W. Rudin, Real and Complex Analysis, McGraw–Hill Book Co., New York, (1987), ISBN 0-07-054234-1.
A. G. Vitushkin, Half a century as one day, Mathematical events of the twentieth century, 449–473, Springer, Berlin, (2006), ISBN 3-540-23235-4/hbk.

Inline citation

↑ Forstnerič, Franc (2019). "Mergelyan's and Arakelian's theorems for manifold-valued maps". Moscow Mathematical Journal. 19 (3): 465–484. arXiv: 1801.04773 . doi:10.17323/1609-4514-2019-19-3-465-484. MR 3993004.
1 2 3 Fornaess, J.E.; Forstneric, F; Wold, E.F (2020). "The Legacy of Weierstrass, Runge, Oka–Weil, and Mergelyan". In Breaz, Daniel; Rassias, Michael Th. (eds.). Advancements in Complex Analysis – Holomorphic Approximation. Springer Nature. pp. 133–192. arXiv: 1802.03924 . doi:10.1007/978-3-030-40120-7. ISBN 978-3-030-40119-1. S2CID 220266044.

External links

"Mergelyan theorem", Encyclopedia of Mathematics , EMS Press, 2001 [1994]
Mergelyan's Theorem -- from Wolfram MathWorld

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[A-1] Forstnerič, Franc (2019). "Mergelyan's and Arakelian's theorems for manifold-valued maps". Moscow Mathematical Journal. 19 (3): 465–484. arXiv: 1801.04773 . doi:10.17323/1609-4514-2019-19-3-465-484. MR 3993004.

[B-2] 1 2 3 Fornaess, J.E.; Forstneric, F; Wold, E.F (2020). "The Legacy of Weierstrass, Runge, Oka–Weil, and Mergelyan". In Breaz, Daniel; Rassias, Michael Th. (eds.). Advancements in Complex Analysis – Holomorphic Approximation. Springer Nature. pp. 133–192. arXiv: 1802.03924 . doi:10.1007/978-3-030-40120-7. ISBN 978-3-030-40119-1. S2CID 220266044.

[1]

[2]